The Other Side of Math
∞ PART SEVEN ∞
CHECKING ANSWERS:
The Student Checks the Answers to
His Own Created Problems
(or HOW TO GET 100% ON MATH EXAMS!)
DEFINITION OF “CHECK”: When you check something, you confirm, make sure or establish that something is true, accurate or acceptable.
 IMPORTANT NOTE
IMPORTANT NOTE
Checking Answers is an integral part of Step 2. However, quite in addition to its connection to Step 2, Checking Answers is an important subject on its own.
 INTRODUCTION:
INTRODUCTION:
THE IMPORTANCE OF CHECKING ANSWERS
Creating Problems (OSOM, Step 2) includes students systematically checking the answers to their own self-created problems.
Why to check, when to check and how to check are essential elements of an individual’s expertise with math. Oddly, it is sometimes considered so minor by authors of some math textbooks that data on checking the accuracy of the solutions to a particular topic is tacked on as an afterthought to that topic. And sometimes checking is simply ignored. The right way is to treat checking answers as an integral part of every topic by including any needed theory, data, examples, exercises and problems to teach this skill alongside a textbook’s lessons on stating, writing, and solving a particular topic.
Because the art of checking answers is often neglected by authors, teachers, students, and examiners, this part (Part Seven) is the longest section of The Other Side of Math.
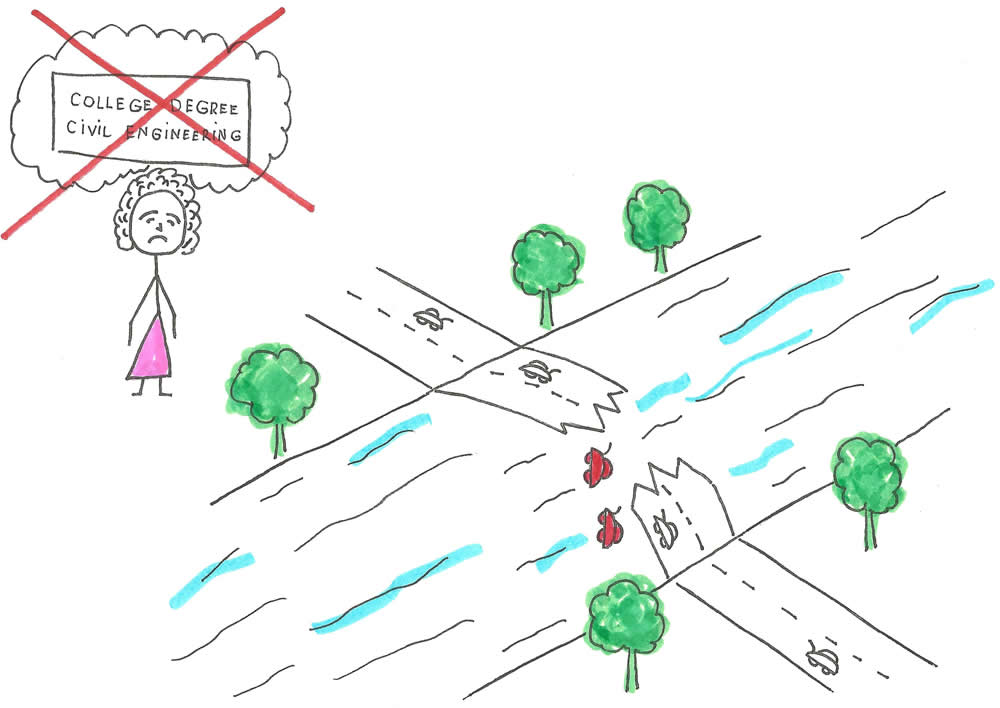
(Except from the Sunday Edition of the Penigawissett News of August 14, 2019)
“The disastrous collapse of the just-opened Penigawissett River Bridge has cut off the East Bank business and industrial district of our fair city from the Oregon National Railway lines on the West Bank…
“…but how on earth will we fill the orders for our paper and lumber products if we can’t deliver them on time?” asked Benjamin Besserin, Senior Marketing Director of Penigawissett Timber Products during a recent interview on the Channel 9 Nightly News Show….
Mrs. Marion Fryye, Chief Project Engineer for the River Bridge and overall supervisor of the structure’s planning and construction, has been removed from post after she admitted approving the construction plans without checking the final calculations. Our reporter requested an interview with Mrs. Fryye but…
 CHECKING ANSWERS
CHECKING ANSWERS
Creating Problems (OSOM, Step Two) includes students systematically checking the answers to their own self-created problems. The skill of checking answers, when practiced, becomes second nature and adds little time to doing math However, for the short time invested, checking answers pays off in the accuracy of results.

This section (Part Seven, Checking Answers) presents general principles and guidelines as well as specific methods for checking the accuracy of solutions to math problems.
Most importantly, it also includes WHY checking is done. Students need to understand the purpose of checking, how it applies to their lives in the real world or they will not learn to check their answers.
These same principles, reasons why, guidelines, methods, purposes are applicable to checking a textbook’s problems as well as the problems students create as part of their OSOM program.
STUDENTS ON THE OSOM PROGRAM MUST CHECK THEIR ANSWERS BECAUSE THERE IS NO ANSWER BOOK FOR THEIR SELF-CREATED PROBLEMS. THE ONLY WAY THEY WILL KNOW IF THEIR MATH IS CORRECT IS BY CHECKING THEIR ANSWERS. THIS IS THE SAME SITUATION THAT STUDENTS WILL FACE IN THE REAL WORLD, THE WORLD OUTSIDE THE CLASSROOM.
IN THE REAL-WORLD, EACH INDIVIDUAL IS RESPONSIBLE FOR HIS OWN MATH, INCLUDING, WHEN NEEDED, CREATING HIS OWN ANSWER BOOK.
 USING MATH TO SOLVE A REAL-LIFE PROBLEM
USING MATH TO SOLVE A REAL-LIFE PROBLEM
The application of mathematics to real-life problems follows a natural sequence:
THE FIRST STEP: SOMEONE BECOMES AWARE OF A PROBLEM OR SITUATION THAT REQUIRES MATHEMATICS TO BE APPLIED TO ATTAIN A SOLUTION.
► Example: A man realizes that the first of the month has arrived and he has a lot of bills to pay.

► Example: An aircraft engineer has just been told she will be designing the wings of a new airplane.
THE SECOND STEP: THE PROBLEM OR SITUATION MUST BE CLEARLY STATED.
►For the man paying household bills, it might be as simple as saying to himself, “How much money is available in my checking account?”

► The airplane designer will be required to make a detailed statement of the purpose and capabilities of the new plane she is designing: “Boeing’s state-of-the-art intercontinental airliner for the 21st Century must fly at an altitude of 70,000 to 80,000 feet, cruise at a sustained rate of 1750 miles per hour and carry a load of 315 passengers with 15,000 pounds of luggage. Now, what should the wings of this plane look like?”
THE THIRD STEP: MATH MUST BE APPLIED TO SOLVE OR HELP SOLVE THE PROBLEM.

THE FOURTH STEP: THE MATH COMPONENT OF THE SOLUTION IS CHECKED FOR ACCURACY.

 Different Levels of Checking Answers
Different Levels of Checking Answers
The math applied in solving a problem may be only one minor component of a complex problem or the math may provide the entire solution.
Checking answers to a math problem does not mean the same thing to each person in every situation. There is no “one size fits all.” There are as many reasons and ways to check answers to math problems as there are individuals living their unique lives.
Here are some examples of checking (and not checking) that span a wide spectrum.
► SOME PROBLEMS REQUIRE THE EXACT APPLICATION OF STANDARD CHECKING METHODS SUCH AS THOSE TAUGHT IN ARITHMETIC, ALGEBRA, GEOMETRY, TRIGONOMETRY, CALCULUS, ACCOUNTING AND ENGINEERING TEXTBOOKS.
An aerospace engineer working on the Mars landing program, which deals with launch times, fuel consumption, orbits, trajectories and the multitude of problems involved in getting to the Red Planet, will use a tremendous quantity of straight mathematics. And he will check EVERYTHING he or she does many (many!) times with computers running software designed for the specific kinds of problems the engineer is facing. At times, he will use his own personal scientific calculator. And he will sometimes use pencil and paper and calculate by hand. Further, when faced with the slightest doubt, he will have others check his calculations. HIS ANSWERS MUST BE 100% CORRECT AND HE KNOWS IT.
An older person who does not have an abundance of money (perhaps because he is living on Social Security income) would probably check his bank account balance to the penny using precise addition and subtraction checking methods.
► SOMETIMES ONE MUST CHECK BECAUSE THE PERSONAL PENALTIES FOR NOT CHECKING ARE TOO GRIM TO FACE.
Consider an individual with a digestive disorder who can only eat certain foods and in exact quantities? She follows her doctor’s orders if she wants to avoid debilitating pain. She measures each and every food item on a digital food scale that measures weights to the tenth of an ounce. Every day and every meal, she checks every measurement by weighing it a second time and marking her actions on a checklist the doctor gave her.
Eventually she learns to trust her perceptions and actions and only weighs foods once. She has stopped double checking her answers because she now KNOWS they are correct. By this time, her perceptions of food quantities and their weights is very high.
One fine day, she realizes that she has her digestive disorder under good control and ceases to even weigh her foods. By sight alone, she can tell if she is using the right amounts. She still checks, but her checking is simple observation of the food as she prepares it. When in doubt, she might occasionally pull out her scale just to be sure.
► SOME PROBLEMS ARE SOLVED AND CHECKED INFORMALLY AND CASUALLY.
A rich person may have no interest in exact balances. The rich person might glance at each entry in his credit card account records or checkbook register, casually and mentally round the entries to the nearest hundred-thousand dollars and wind up with a vaguely approximate round number. For him, knowing he owes “about $800,000.00” is good enough.
► THERE ARE MANY SITUATIONS WHERE ONE SIMPLY DOES NOT CHECK THE MATH AT ALL BECAUSE THE INDIVIDUAL’S JUDGMENT AND CERTAINTY IS SUCH THAT HE KNOWS HIS MATH IS CORRECT.
John gets up at 6:00 A.M. to prepare for a long day of work. He knows from years of experience that he can accomplish each of his early morning tasks and chores between the hours of 6:00 A.M. and 8:00 A.M., at which time he must walk out the front door of his condo in Waban, Massachusetts, climb into his 2005 Honda Civic to start the daily commute into downtown Boston. His math calculations concerning time ARE correct and he knows is it.
►AND THERE ARE ALL THOSE TIMES WHEN IT DOES NOT MATTER WHETHER ONES’ MATH IS CORRECT OR NOT.
A woman loves to create new dishes for her family. She habitually experiments with spices and special ingredients. She is blessed with a husband and kids who eagerly await each new version of her unique spaghetti sauce or salad dressing. Why should she bother counting shakes of the ginger and turmeric dispensers as she dances through her fully-equipped, gourmet kitchen, creating as she goes? (Of course, most families are not as tolerant of changes to their favorite dishes.)
 Silly Math Errors
Silly Math Errors
Definition of “Silly Math Error”: A silly math error is a mistake in calculation made not because the individual misunderstood the math needed to solve the problem correctly but only because he did not bother to check his answer. Had he checked his answer, he would have clearly seen his silly math error and been able to correct it using only the knowledge and skills he already possessed.
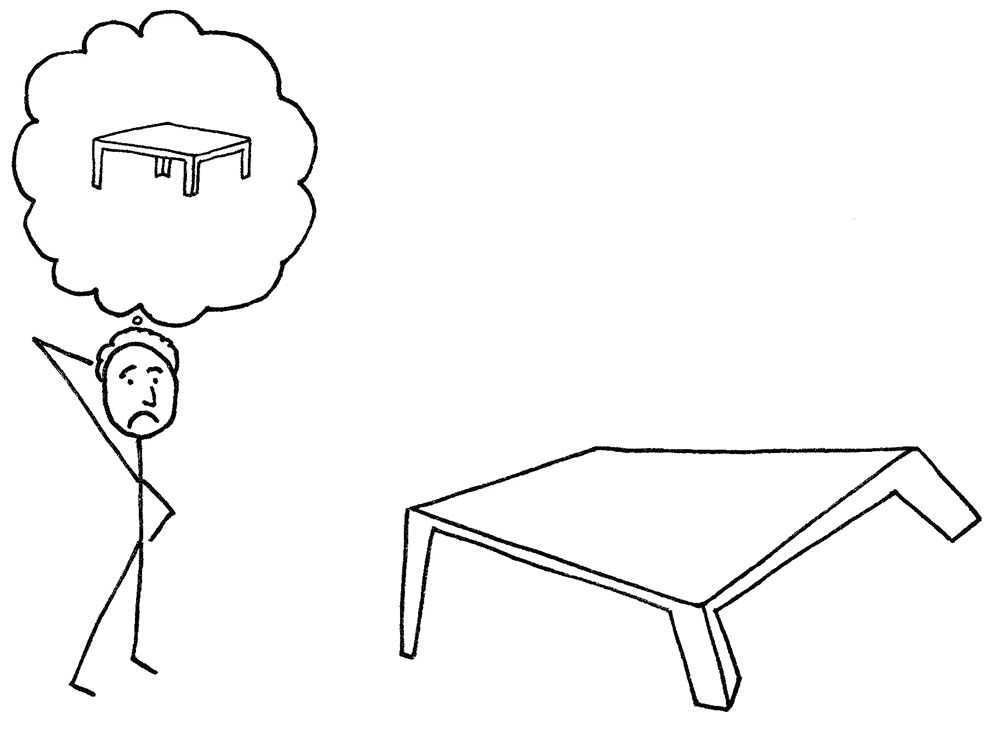
As a tutor working in a busy K-12 school helping kids in trouble learning math, I have a bird’s-eye view of the purpose and value of checking the accuracy of answers to math problems. One of my duties is helping students who have done poorly on their math exams. That’s when I roll up my sleeves and dig deep to find out exactly what is really causing the math errors. I continue working with a student until he has mastered the math he previously did not understand and can apply it correctly.
Because of the part I play in the correction of math exams, I know exactly – in the greatest detail possible – what can go wrong in learning and applying math. Further, I know how to turn the student’s confusion and uncertainty into knowledge and skill.
I have made the following observation time and time again: while taking exams, students commonly make a combination of “silly math errors” and errors caused by genuine confusions on specific math concepts and procedures. Although it is uncommon for a student’s errors in math exams to be only the “silly math errors” kind, that has happened, too.
From this experience, I have gained an important fact: REGARDLESS OF HOW BADLY A STUDENT HAS DONE ON A SPECIFIC MATH EXAM, THAT STUDENT’S EXAM RESULT WOULD ALMOST ALWAYS HAVE BEEN BETTER – SOMETIMES MUCH BETTER! – HAD HE SIMPLY CHECKED HIS ANSWERS. Why? Because had he checked his answers he would have clearly seen and been able to correct his silly math errors.
In other words, the very fact of checking his answers would have improved his accuracy – totally aside from any confusions he had on his lessons. After fixing literally hundreds of math exams, there have been very few exceptions to the above statement.
 MATH ERRORS IN THE WORK-A-DAY WORLD
MATH ERRORS IN THE WORK-A-DAY WORLD
Making silly math errors has consequences beyond the taking of elementary, middle or high school math exams. Remember, school is a safe and forgiving place to learn in. The story is quite different once the student graduates and takes his place in the work-a-day world.
Soon after a 30-year mortgage is closed, it is discovered that the new homeowner cannot sensibly afford to repay the loan.

Too many silly mistakes and that home improvement project worked on for days or weeks fails because some critical lengths of wood and metal were not cut to the correct length.

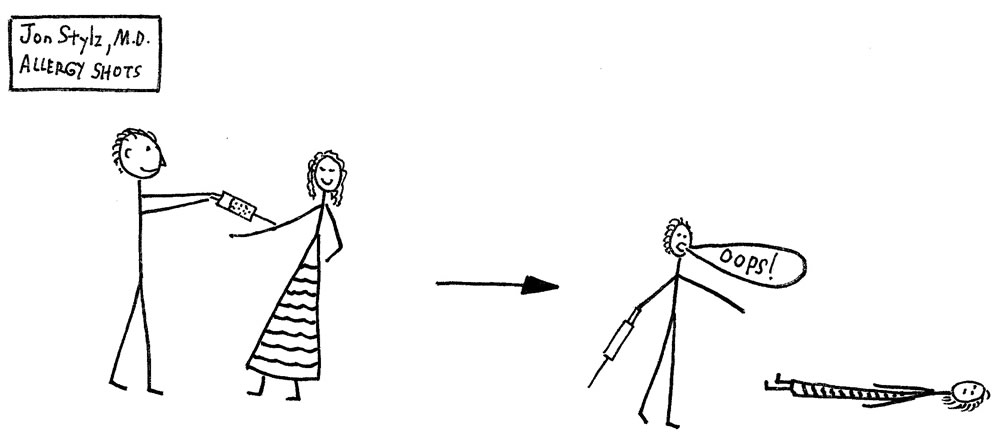
Or the medical doctor loads too many (or too few) cubic centimeters of medicine into the syringe.
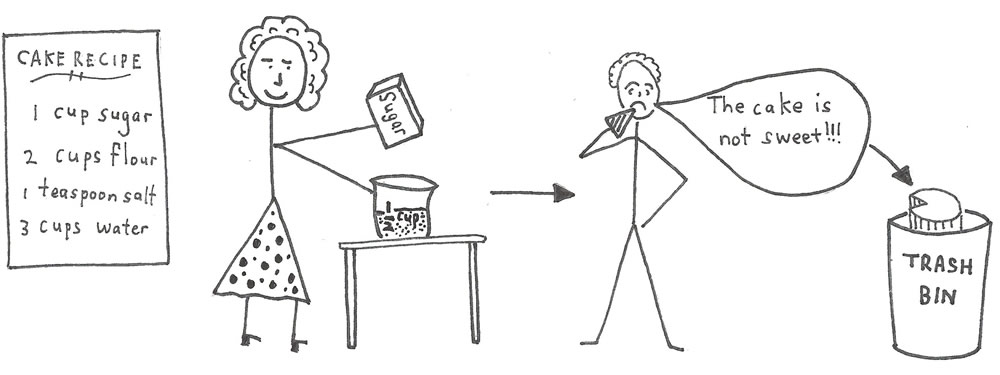
Too many silly math errors and even the best recipe using the finest ingredients can turn into a culinary disaster.
Or, finally, the civil engineer’s bridge drops into the river carrying with it a few carloads of people.

While it may be true that the bridge designer, the cook, the doctor and the new homeowner were confused about the actual math or that they had evil intentions or were outright criminals, it may also be true that they did understand the math involved, were decent people but were simply “too busy” and neglected checking their calculations – with disastrous consequences. Regardless of why they accepted wrong answers, the bridge engineering supervisor may never get another chance to build a bridge, the homeowner will likely lose his home, the cook had a bad evening with her disappointed family, and the doctor’s patient may not get better – or may die!
So, in the long term, why should students check answers? The short answer is:
TO LIVE BETTER
If a worker or executive in any field values his job, clients, paycheck, home and kids, friendships, bank account and life, he checks the accuracy of his important calculations. He knows that if he wants to arrive home unscathed after a hard day’s work, he must somehow ensure that his important answers are correct.
And even when he is safe and sound at home, he must still continue to ensure that his answers to important non-work calculations are also correct.
The conclusion is obvious: STUDENTS MUST LEARN NOT ONLY HOW TO CHECK THEIR SOLUTIONS BUT THEY MUST LEARN HOW TO CARRY OUT THIS ASPECT OF A COMPLETE MATH EDUCATION ACCURATELY, SWIFTLY AND PROFESSIONALLY.
 SHOULD THE FULL SKILL OF CHECKING ANSWERS
SHOULD THE FULL SKILL OF CHECKING ANSWERS
BE A REQUIRED PART
OF EVERY MATH CURRICULUM?
Curriculum developers and the authors of math books correctly emphasize getting right answers to the book’s problems. Appropriately, math examinations test the student on the correctness of his solutions. But shouldn’t the student also be examined on his skill and accuracy in checking the solution? After all, when he is out of school and in the real world isn’t he responsible for getting right answers? How does he know he is right when there is no teacher nearby and no answer book?
Math books almost always teach the solution method for a specific kind of problem, but the same books do not always teach an appropriate checking method for that type of problem. Oddly, some math books do teach good checking methods but then do not require that students apply checking to their problems.
So if a student’ textbook or teacher does not teach or require exact methods of checking answers for a specific type of problem, the student must put on his thinking cap. The following sections will assist students to develop thinking processes that arrive at a variety of valid methods of checking answers.
Note carefully: The following thinking patterns and procedures are the ones I have learned from the authors of my math courses or have developed myself. These patterns work for me. That means they confirm whether my answers are correct or incorrect — in which case I (groan!) start again! It is likely that your textbook and teacher can offer you others.
Also (and importantly) you can invent your own way to check your problems unless your teacher or book requires a certain method.
 THE ART OF CHECKING ANSWERS
THE ART OF CHECKING ANSWERS
FOR THE SIX BASIC OPERATIONS
Definition of “Operation”: In its simplest form (in arithmetic), an operation is a mathematical process in which numbers are derived from other numbers through the application of definite rules. In algebra, not only numbers (constants) but letters representing unknown numbers (variables) or a combination of constants and variables are often involved in operations.
Addition, subtraction, multiplication, division, raising to a power, and finding roots are the most common arithmetic operations.
Definition of “Inverse”: The inverse of one operation (for example, addition) is another operation (for example, subtraction) that cancels what the first operation has done.
Definition of “Undo”: To cancel or reverse the effect of an action” (Reference: The Encarta Dictionary of the English Language).
Here is “undo” used in sentences: “The division operation can be used to undo a multiplication operation.” “The addition operation can be used to undo the results of any subtraction operation.”
How does this work?
FIRST: WE START WITH 8 APPLES.
THEN: WE SUBTRACT 3 APPLES.
FINALLY: WE GET A DIFFERENCE OF 5 APPLES.
THE ABOVE SEQUENCE (first, then, finally) IS THE ACTION AND THE EFFECT OF USING THE SUBTRACTION OPERATION.
Now, to reverse that action, to undo that action, we ADD the 3 apples back into the difference of 5 apples.
5 apples PLUS 3 apples = 8 apples!
Yippee! The effect or result of the subtraction operation has been reversed by the use of the addition operation because we are back where we started with our original amount of 8 apples!
▓ CHECKING ANSWERS WHEN DOING ADDITION ▓
WHEN DOING ADDITION, you use the inverse operation, subtraction, to check your answer because subtraction undoes (reverses) addition. That means if you start with the number 25 and add 36, you get a sum of 61. If you then subtract 36 from the sum of 61, you are back to your original number, 25. The effect of adding 36 was nullified by subtracting 36 from the sum of 61.

Of course, if you do NOT arrive back at your original number of 25, then you know you made a mistake and must take action to find your error.
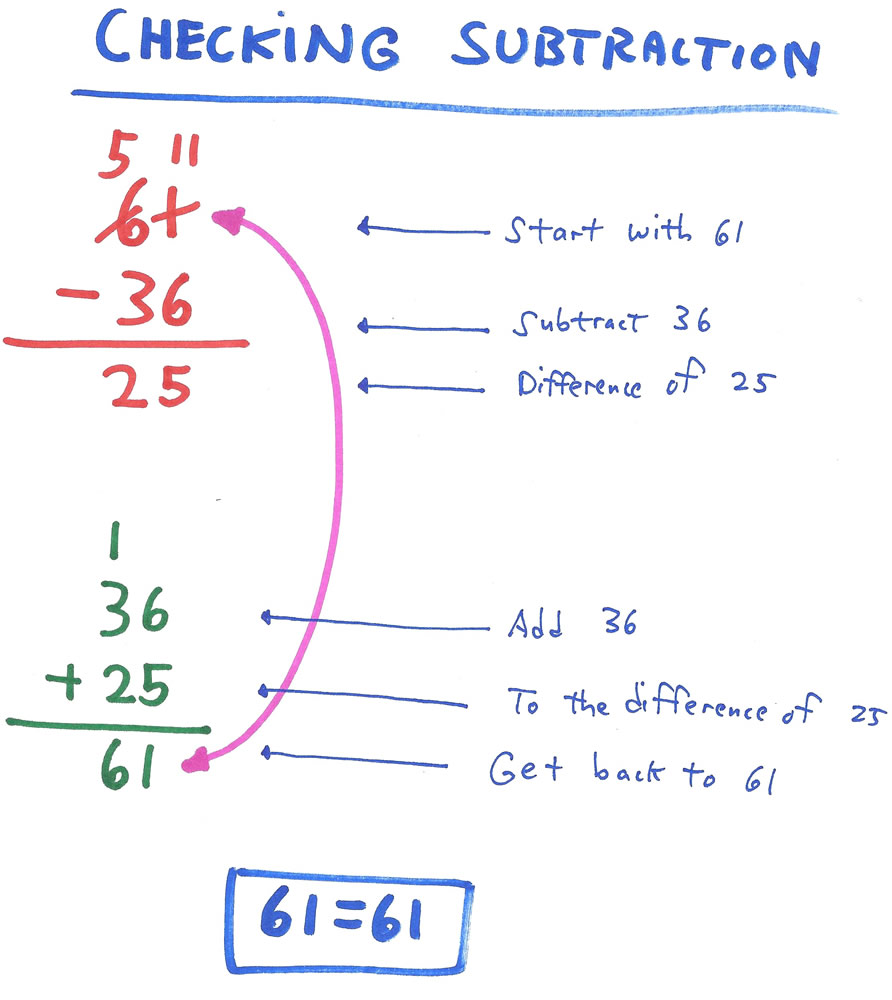
▓ CHECKING WHEN DOING SUBTRACTION ▓
WHEN DOING SUBTRACTION, you use the inverse operation of addition to check your answer. Addition undoes (reverses) subtraction. That means if you start with the number 61 and subtract 36, you get a difference of 25. If you then add back the 36, you get your original number of 61. The effect of subtracting 36 from 61 was canceled out by adding back the 36.
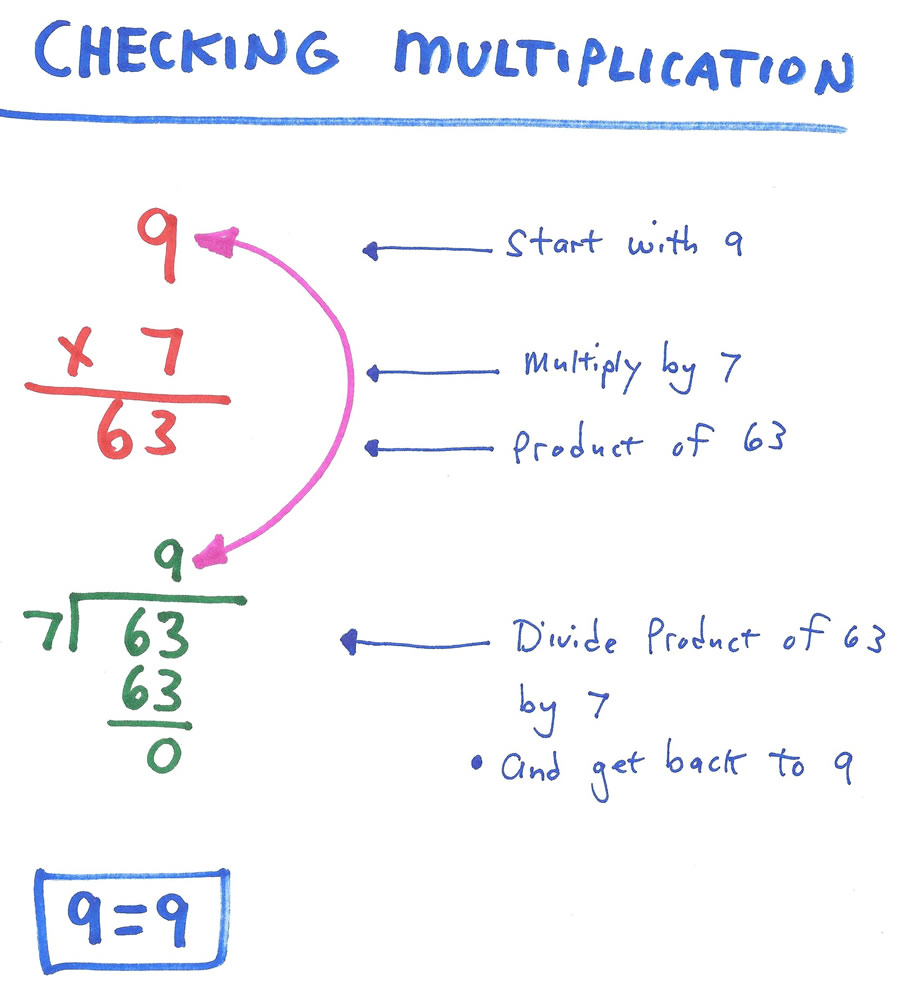
▓ CHECKING WHEN DOING MULTIPLICATION ▓
WHEN DOING MULTIPLICATION, you use the inverse operation of division to check your answer because division undoes (reverses) multiplication. If you start with the number 9 and multiply 9 by 7 you get a product of 63. If you then divide the product of 63 by 7, you are back to 9, your original number. The division nullified or canceled out the effect of multiplying.
▓ CHECKING WHEN DOING DIVISION ▓
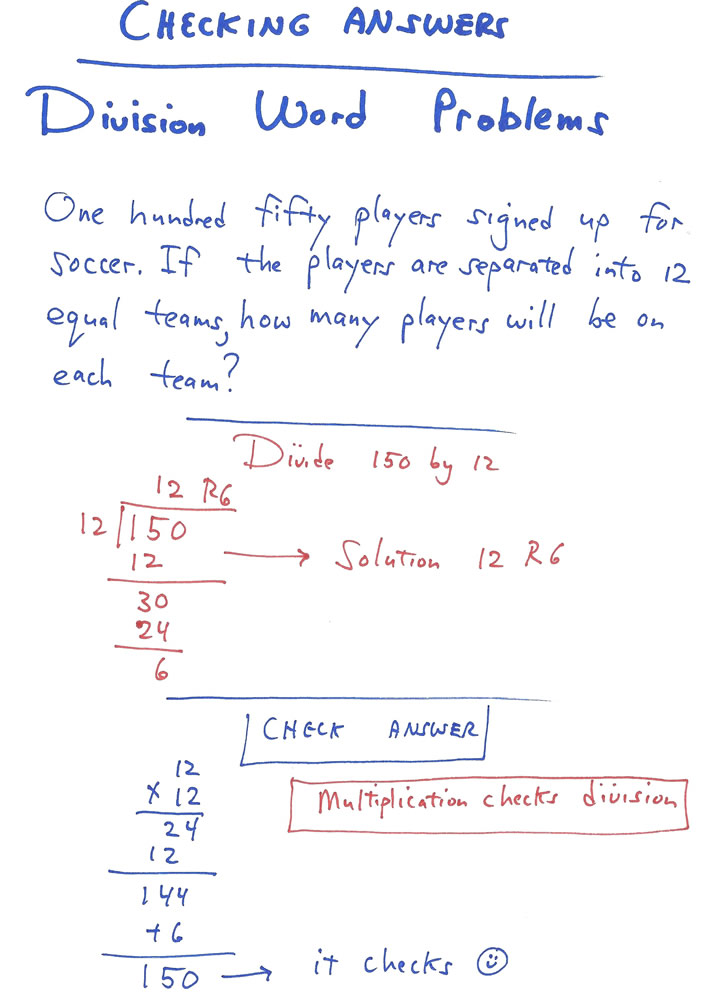
WHEN DOING DIVISION, you use the inverse operation of multiplication to check your answer because multiplication undoes (reverses) division. We start with a dividend of 63 and divide that by 7. We get a quotient of 9. If you then multiply that quotient of 9 by 7, you are back to 63, your original number. By using the inverse operation of multiplication, the effect of dividing by 7 was canceled out.

Here’s an example of using an inverse operation to check the answer to a 4th grade division word problem:
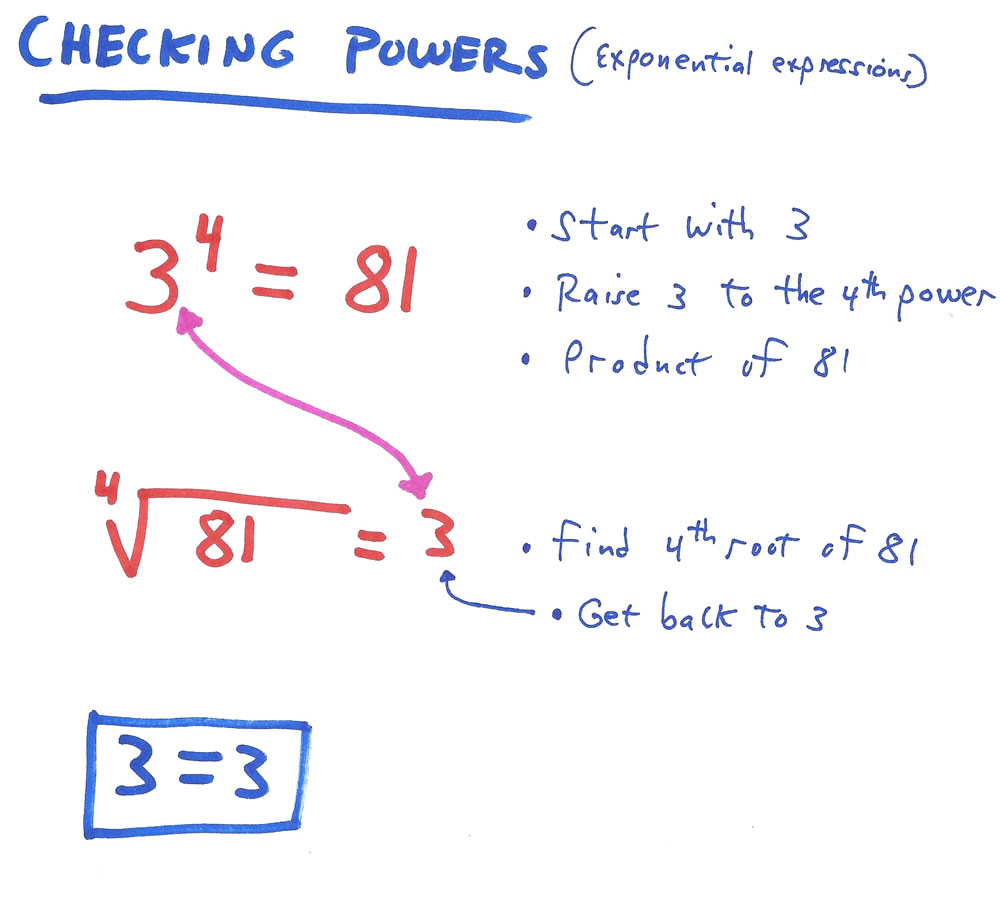
▓ CHECKING WHEN RAISING A NUMBER TO A POWER (or CHECKING WHEN USING EXPONENTIAL EXPRESSIONS) ▓
WHEN RAISING A NUMBER TO A POWER, you use the inverse operation of “finding roots” to check your answer, because finding roots undoes (reverses) raising a number to a power. If you start with the base of 3 and raise it to the 4th power, you get a product of 81. If you then find the 4th root of 81, you have arrived back at your base, 3. The action of finding a root cancels out the effect of raising a number to a power.
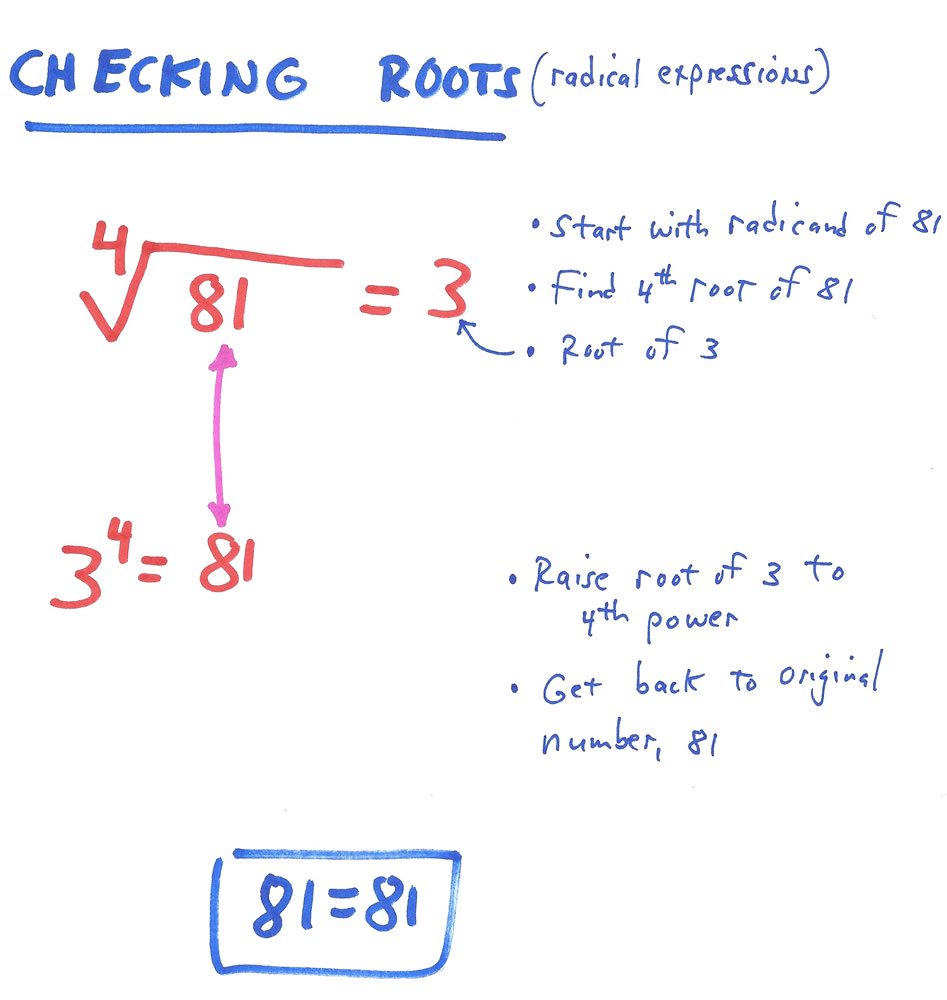
▓ CHECKING WHEN FINDING ROOTS ▓
WHEN FINDING ROOTS, you use the inverse operation of raising to a power to check your answer because raising to a power undoes (reverses) finding a root. If you start with a radicand of 81 and find the 4th root, you get a root of 3. If you then find the 4th power of 3, you get back to your original number of 81.
 CHECKING BY REVERSAL:
CHECKING BY REVERSAL:
CONVERTING THE SOLUTION BACK TO THE ORIGINAL PROBLEM
On Step Two of OSOM, when a student has mastered a topic, he creates his own problems for that topic, solves his problem and checks his answers. The following are examples of how to check solutions by working back from the solution to the original problem.
▓ SECOND GRADE: CHECKING A FACT FAMILY ▓
A fact family is four math facts (two addition facts and two subtraction facts) made using the same three numbers. To create a fact family, the student chooses three numbers which will be used to write two addition facts and two subtraction facts. The student must choose the three numbers carefully. The first two numbers must add up to the third number (e.g. 3 + 5 = 8). 
He makes a little table and, at the top, writes the three numbers he has chosen for his fact family.

He writes his four facts.

To check his table of four facts, he thinks in reverse. He chooses just one of his facts and writes that fact in a new table.
Starting from just that one fact, he writes his entire fact family. If his new table matches his original table, he was correct.

▓ SIXTH GRADE:
CHECKING A FRACTION CONVERSION TABLE ▓
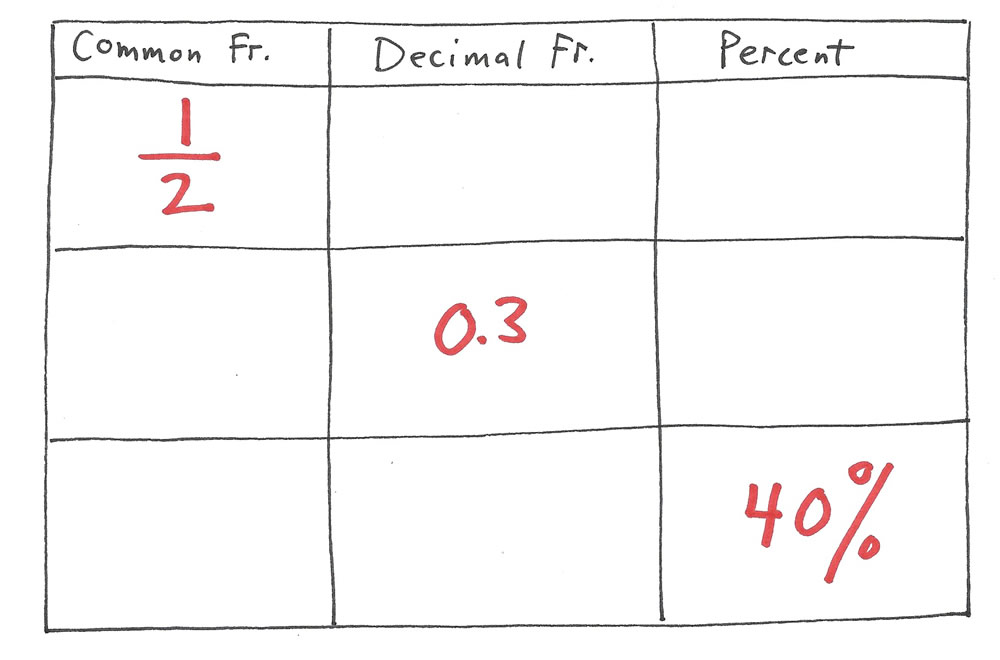
In the 6th grade, most students are learning how to convert each of the three kinds of a fraction (common fraction, decimal fraction or percent) to the other two forms of a fraction easily, quickly and accurately. A student’s invented problem, solution and checking might look something like this:
First: The student creates three fraction problems using a fraction table. Only one fraction is given for each line. The student must convert that fraction to the other two equivalent forms.
Second: The student solves his problem by finding the other two equivalent fractions
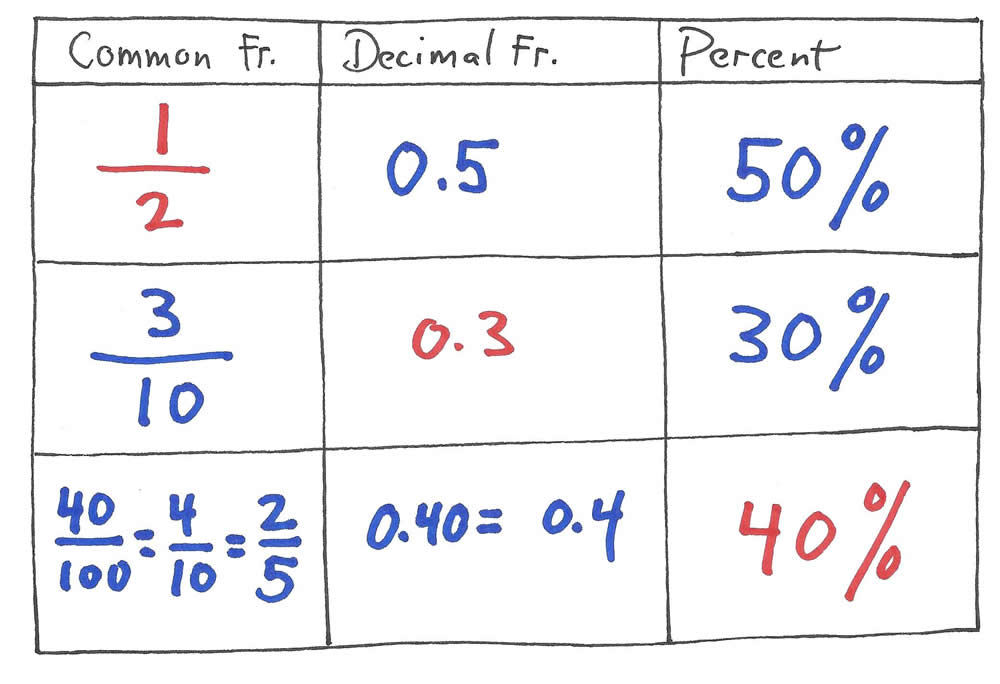
Third: To check his created problem, the student makes a new fraction table and writes in only his solutions, intentionally leaving out the original problem. 
Fourth: He checks his solution by finding the original problem (in red). If he works back to his original problem, then his solution was correct.

▓ ALGEBRA TWO:
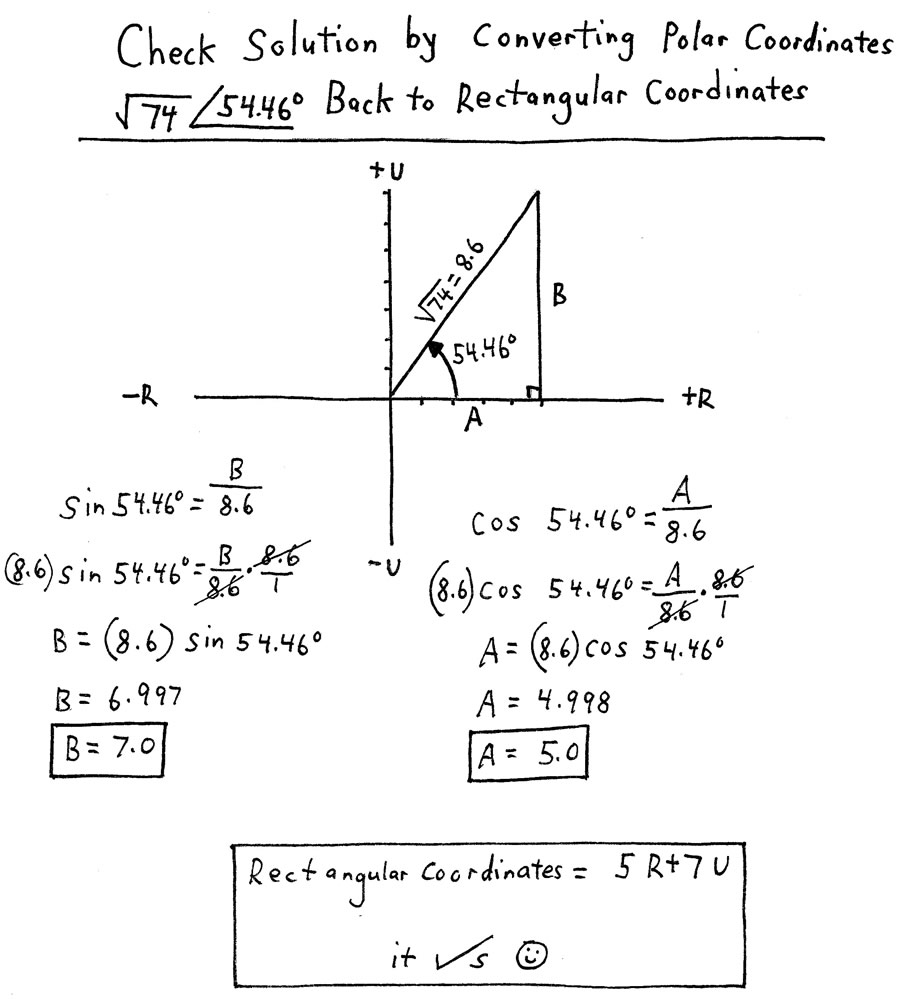
CHECKING POLAR COORDINATES ▓
In Algebra Two, students learn to convert Cartesian coordinates to polar coordinates.
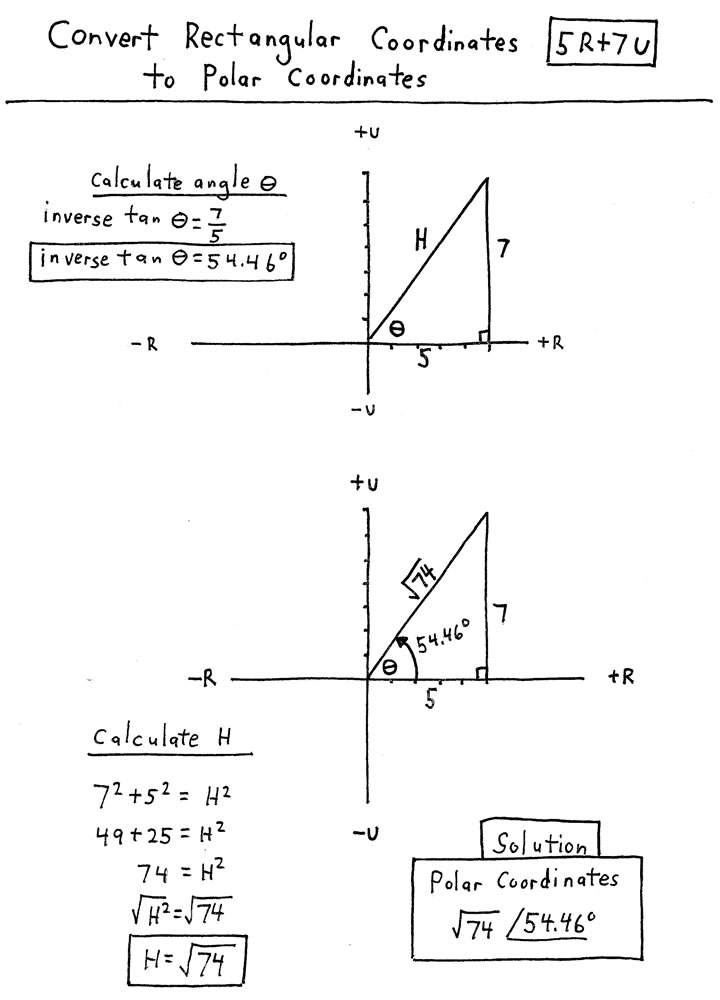
Then, by converting from polar coordinates BACK to Cartesian coordinates, the student has checked the solution to his own created problem.
 CHECKING ANSWERS IN ALGEBRA
CHECKING ANSWERS IN ALGEBRA
In Algebra, there are two broadly useful methods of checking solutions.
▓ ONE: CHECKING EQUATIONS BY SUBSTITUTION ▒
Equations you have solved can be checked by applying the substitution axiom:
► You found certain value(s) for the variable(s) in the equation. Now substitute those same values you found back into the original equation.
► Evaluate the original equation using your value(s).
► The number(s) you arrive at on the right and left sides of the equals sign will match if your answer is correct.
Here’s an example of checking the answer to an equation by substitution. (This is the same example used to demonstrate Problem Creation in Pre-Algebra.)

Here’s an example of checking a more complicated problem in Algebra 1, a rational equation. The left hand column has the solution. Now notice the right hand column where the solution was checked. This example indicates that it sometimes takes more thought, time and effort to check a solution to an equation, compared to just solving the problem. Positive integers are relatively easy to check. Negative integers are a bit more difficult. Fractional answers (including decimal fractions and percents) usually require even more work. But the thought and effort applied to checking solutions inevitably results in greater learning.
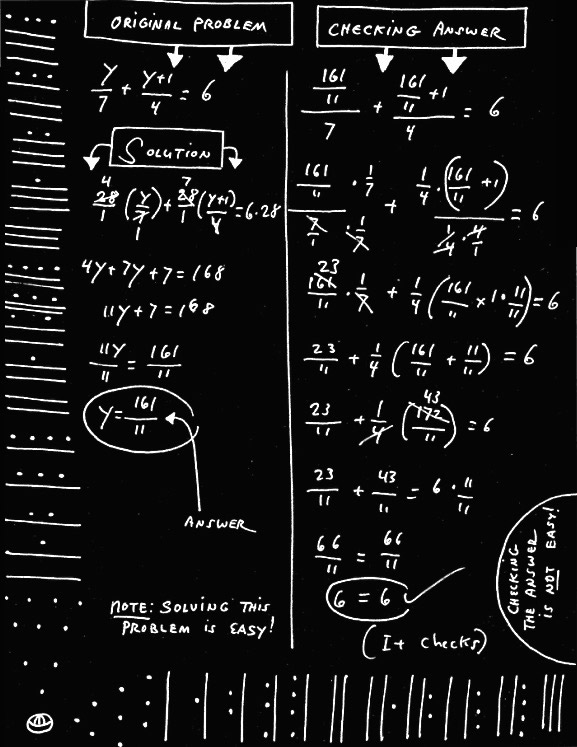
Checking a Rational Equation
CHECKING THE COMPLEX-NUMBER SOLUTION
TO QUADRATIC EQUATION

Here’s the usual, completing-the-square procedure for solving the problem:
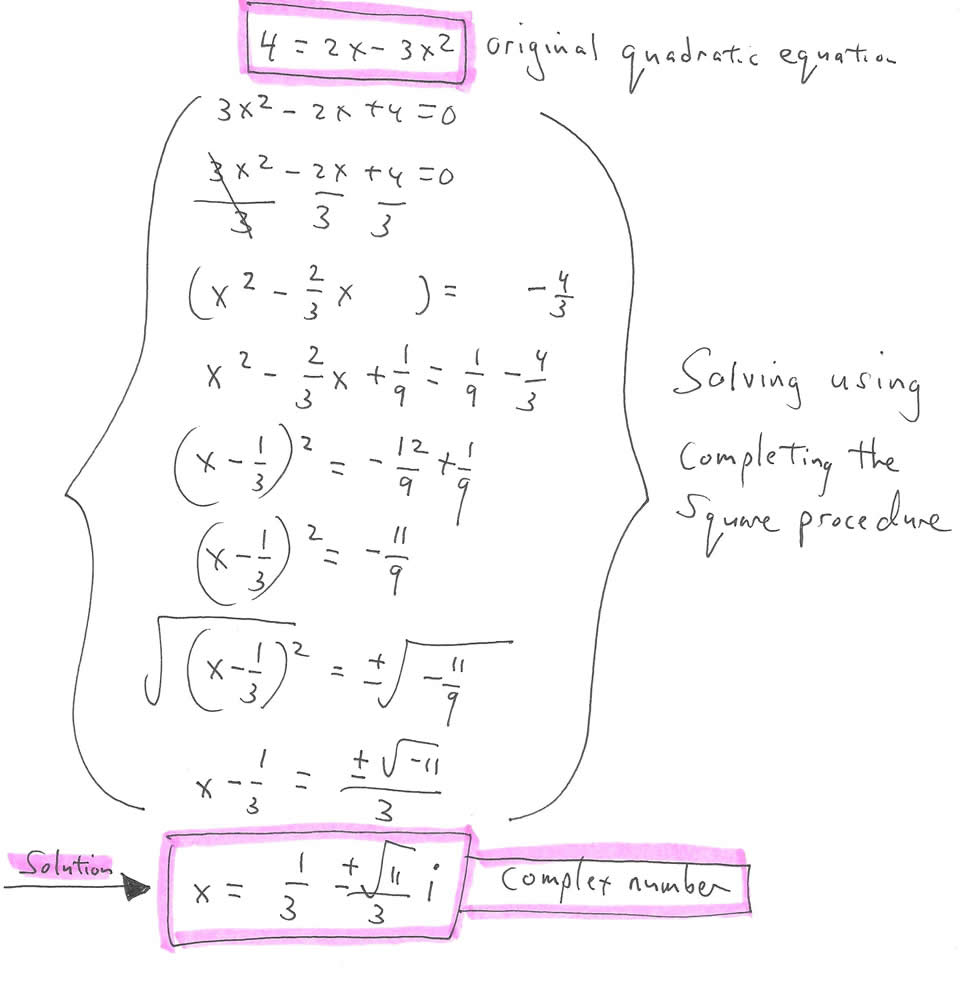
Now the complex-number solution to that problem is checked by substitution:
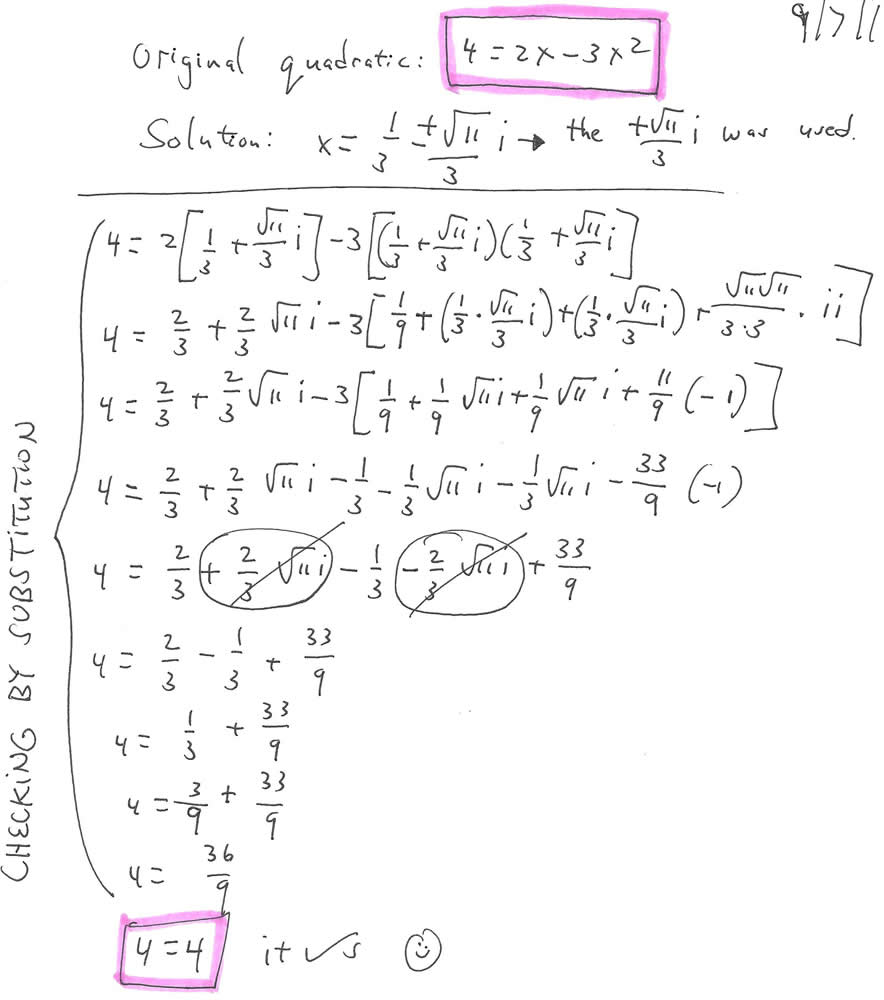
▓ CHECKING SIMPLIFIED EXPRESSIONS THAT CONTAIN VARIABLES ▒
DEFINITION OF “EXPRESSION”: An expression is a single numeral or symbol (like 5 or 5,000 or y or p) or a meaningful group of symbols (like 2p + x3 or 3y + 226qx) that has a single value.
After you have simplified an expression containing variables, choose easy-to-use numbers such as 2, 3, 4, 5, etc., to replace the variable(s). Caution: Since division by zero is undefined, ensure that the numerators of any fractions do not evaluate to zero. Also, if any terms evaluate to zero you will probably not be able to check your solution. So, just ensure that your terms have a value greater than zero and that your numerators are not zero.
► Substitute your chosen numbers for the variable(s) into both the original expression and the simplified expression.
►Third, evaluate both the original expression and your simplified expression using the same value(s) for each variable. The final value of the original expression and the final value of the simplified expression will be the same if your simplification was done correctly.
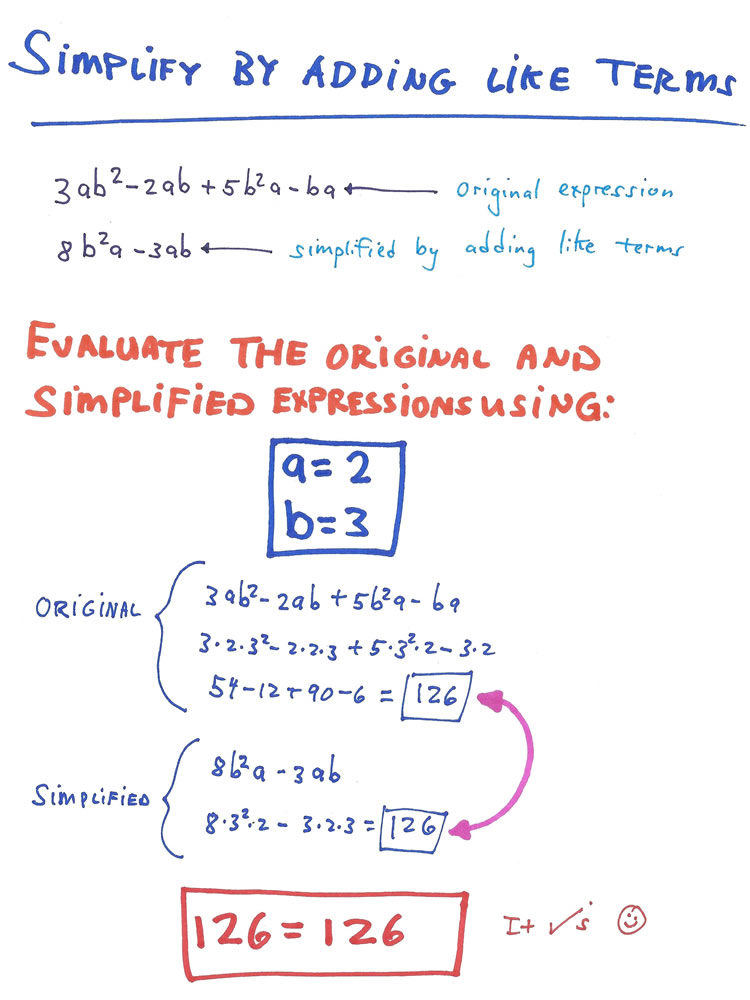
▓ EXAMPLES OF CHECKING SIMPLIFICATIONS ▒
CONTAINING VARIABLES
In Pre-Algebra courses, the student learns to simplify expressions by adding like terms:
This next example (from Algebra 2) demonstrates simplifying a complex fraction — a fraction which contains more than one fraction line. Because the simplification procedure is rather long, only the original complex fraction and the final simplified expressions are given and evaluated:

▓ USING A CALCULATOR TO CHECK SIMPLIFIED EXPRESSIONS THAT CONTAIN ONLY NUMERALS ▒
I often use a scientific calculator to check simplifications of expressions containing numerals and no variables. In the following example, a radical expression with a nested radical is simplified using fractional exponents. Rather than round my answer to the usual 2 decimal places, I calculated to 9 decimal places. I sometimes find this helpful when comparing two such expressions. Occasionally, the last (9th) decimal place will be different.

▓ CHECKING BY GRAPHING SOLUTIONS ▒
GRAPHING CAN BE USED TO CHECK SOLUTIONS TO LINEAR EQUATIONS.
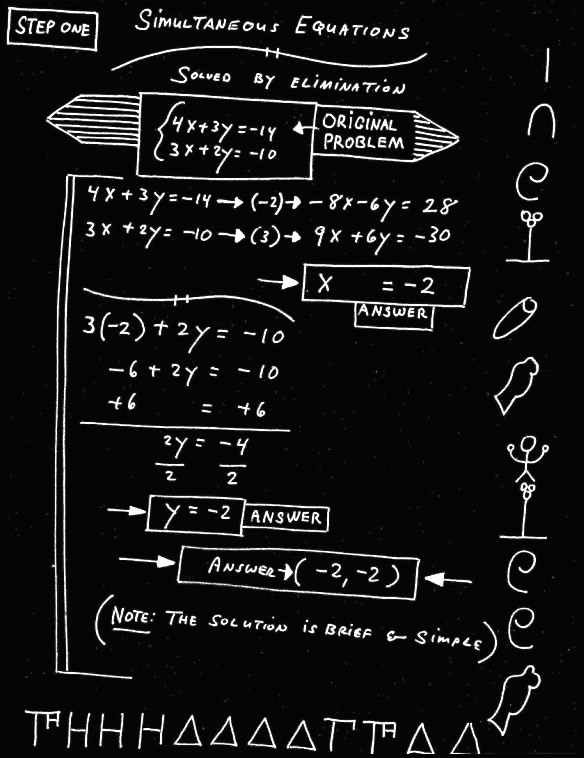
In Algebra One, the student learns to solve a system of two simultaneous equations by three methods: elimination, substitution and graphing. The graphing method can be used to check the elimination and substitution solutions.
In the first illustration, the simultaneous equations are solved by elimination:
In the second illustration, the same pair of simultaneous equations is solved by substitution:

In the third illustration, using the same pair of simultaneous equations, values are given to the x and y variables in preparation for graphing. A table is used for each equation in the system.
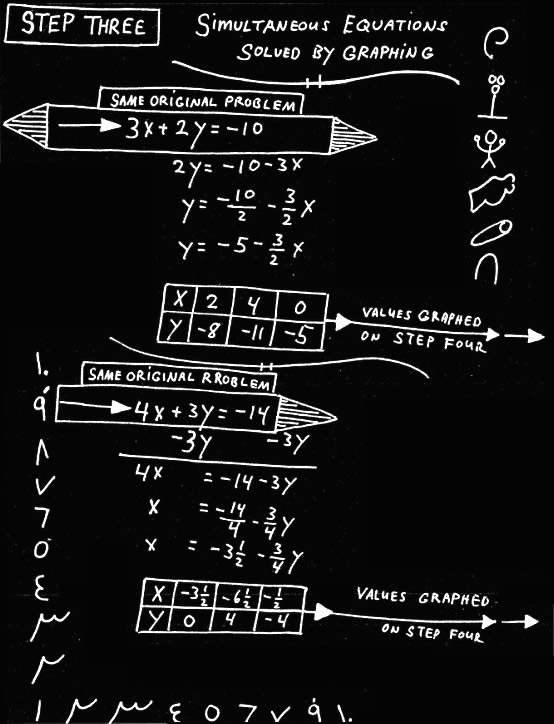
In the fourth illustration, the values of x and y in the two linear equations are graphed. The point where the two lines intersect is the common solution to the system. The graph confirms that the solutions gotten by elimination and substitution are correct:
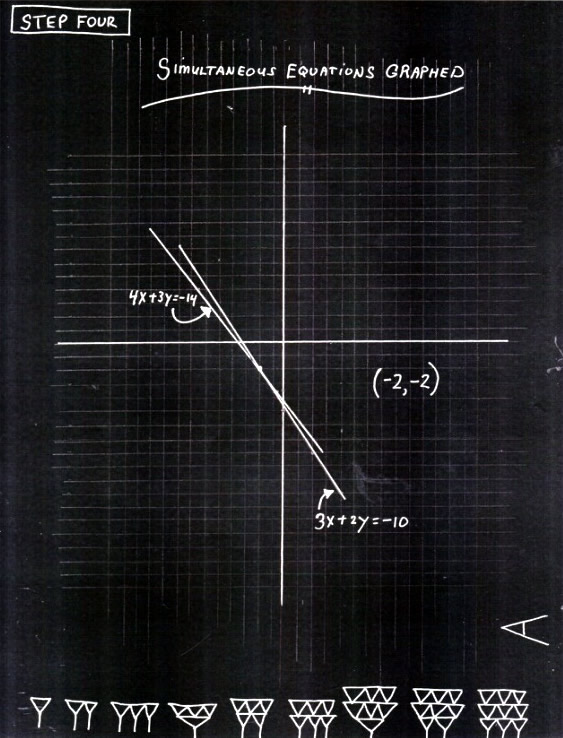
▓ CHECKING BY USING ALTERNATIVE ALGORITHMS ▒
Students often learn alternative algorithms to solve specific types of Arithmetic, Algebra, Geometry and Trigonometry problems. When they know two (or more) such algorithms to solve the same problem, one algorithm can be used to solve the problem and the other can be used to check the answer. The following examples of using alternative algorithms to check answers are just a few of the many possibilities.
QUADRATIC EQUATIONS
Some quadratic equations can be solved by using the zero-factor theorem. All quadratic equations can be solved by completing the square or using the quadratic formula. Use one method to solve the problem and another method to check your answer.
SIMILAR TRIANGLES
The measures of missing sides of similar triangles can be determined using the scale factor. Missing sides can also be determined by the use of proportions; since all three pairs of corresponding sides of similar triangles have the same ratio, these three equivalent ratios can be formed into a proportion and the missing sides found by cross multiplication. The student solves by either scale factor or proportion and checks using the other method.
DIRECT AND INDIRECT VARIATION
Both direct and indirect variation problems can be solved by finding the constant of proportionality or by setting up a proportion using equal ratios. (I have shown only the general form of the two methods.
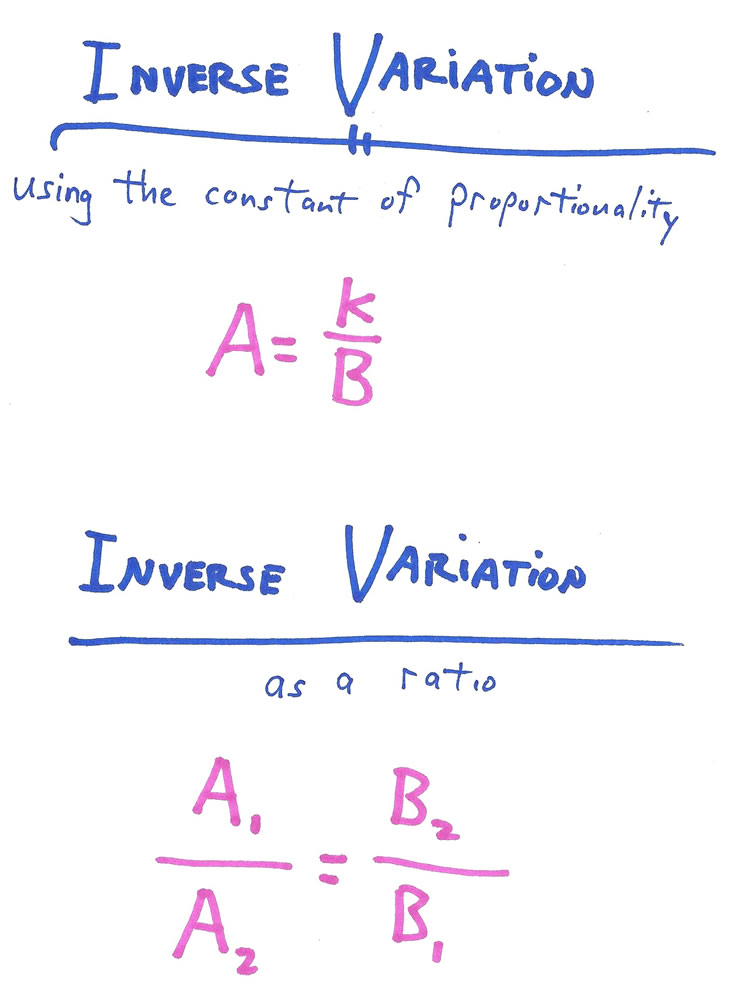
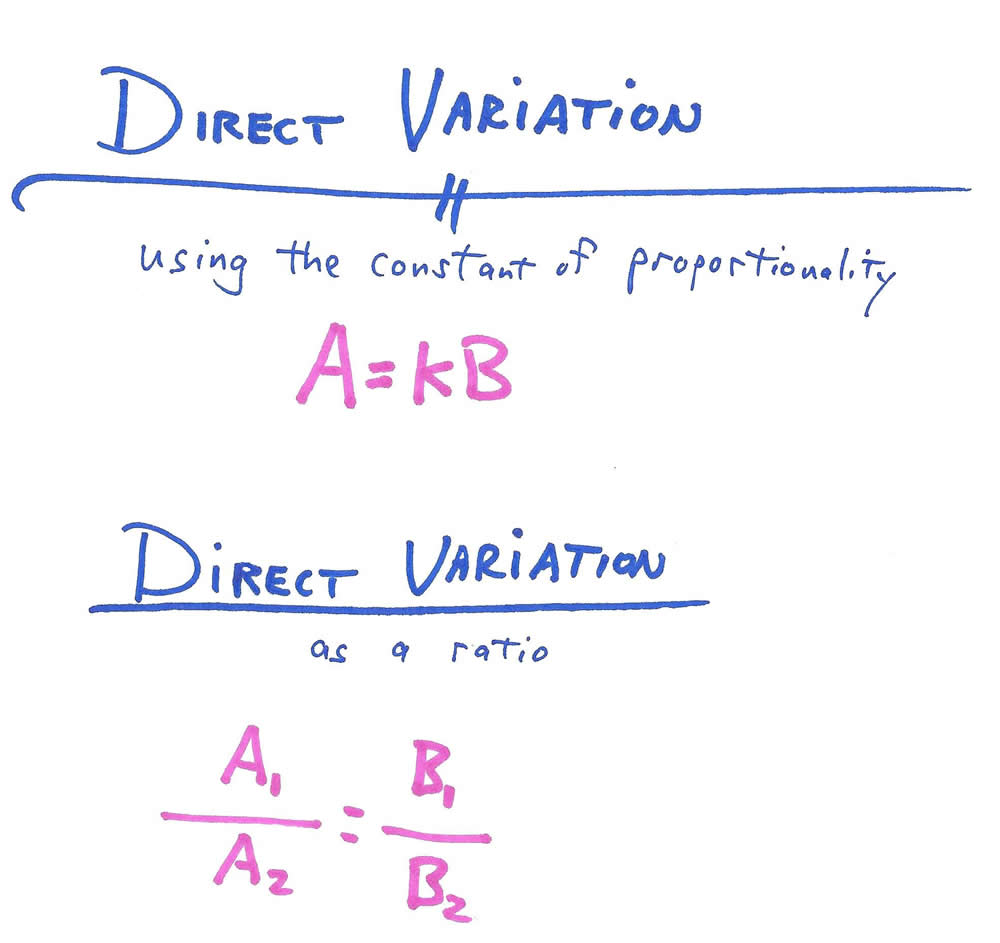
Once again, the student solves by one method and checks by the other.
CHECKING SOLUTIONS IN GEOMETRY
I do not accept the truth of the math in my books without testing the various concepts and procedures for myself.
To prove for myself that measurements in the real world agree with the “math world” described by my textbooks, I often check geometry postulates, theorems and definitions by accurately drawing out the problems and solutions using the exact same specific angles, segments, etc. given in a problem. If my geometric solution is correct, the actual measurements on my drawing paper will be the same as the measurements made using geometric rules and algebraic calculations. Only then do I know the math is true.

On my 8 ½ x 11 paper, this is an accurate 7 inch square. By actual measurement using a ruler, the diagonal did in fact equal the product of the length of a side and .

AND WHEN YOU CANNOT CHECK YOUR ANSWER BY ANY OTHER METHOD?
What do you do when you cannot check your answer by any other method or you are pressed for time? Just redo the problem. SOLVE IT AGAIN AS IF YOU NEVER SOLVED IT BEFORE. That means taking a new piece of paper (or turning your paper over) and without looking at your original solution method or answer, solve it again. If your second answer matches your first answer, you’re probably right. (I say “probably” because you can — as I have done — make the same mistake twice and get the same wrong answer!)

