The Other Side of Math

∞ PART SIX ∞

THE STUDENT SOLVES
HIS OWN CREATED PROBLEMS

 

DEFINITION OF “SOLVE”: IN MATHEMATICS: TO WORK OUT THE SOLUTION TO AN EQUATION OR OTHER MATHEMATICAL PROBLEM.

 

 

IMPORTANT NOTE

 

THE LAST PART, PART FIVE, CONCENTRATED ON THE CREATION OF MATH PROBLEMS, BUT ALSO INCLUDED THE SOLUTIONS TO THOSE PROBLEMS.

IN PART SIX, GREATER ATTENTION IS GIVEN TO ESSENTIAL DATA CONCERNING JUST SOLVING MATH PROBLEMS.

 

 

IS THE STUDENT SOLVING HIS CREATED PROBLEM CORRECTLY?

After a student has created his own problem and written that problem correctly on paper, his next action is to solve that problem.

In the subject of mathematics, there are usually a number of valid methods to solve a particular type of math problem.  Each valid method arrives at the correct answer. But until the student can apply the book’s method exactly, I don’t let him stray one inch from the procedure given in his textbook.

WHATEVER METHOD HIS TEXTBOOK USES TO SOLVE THAT KIND OF PROBLEM IS THE STANDARD I USE TO JUDGE WHETHER OR NOT HE IS SOLVING HIS OWN PROBLEM CORRECTLY.

 

 

 

WHEN THE TEXTBOOK NEEDS HELP

 

Now and again, the book’s solution for a topic (1) leaves out necessary steps and/or (2) fails to give adequate reasons for a step. This can cause students to get lost.

If (1) or (2) is the case, it is ultimately the math teacher’s job to fill in the holes. The teacher must ensures that each of his students has, in writing, the complete, correct solution procedure with the axioms, theorems, rules and definitions justifying all the steps. This gives the student a standard procedure which can then be used for determining correctness of a student’s solution.

Again, this does not mean that the book’s procedure is the only procedure to solve that problem — or even the best way. But it is what the student has just learned. When the student then takes an examination, he must show every step of the solution and those steps are the steps he learned in his textbook.

Once my student has truly mastered the book’s solution — and I know he has mastered it – I don’t worry too much if he then stops writing down each individual step in a solution procedure, starts using mental math and finds his own clever shortcuts or alternative solutions.

 

 

 

DRILLING THE BOOK’S SOLUTION METHOD

When I am teaching a student to solve a problem, whether it is the book’s problem or his own created problem, and he makes errors while solving it, I have him re-do the exact same problem – same numbers, same signs, same everything – over and over.

I DRILL THE SOLVING OF THAT EXACT PROBLEM BY THE BOOK’S METHOD UNTIL HE CAN DO IT RIGHT WITHOUT THE SLIGHTEST ERROR OR HESITATION.

In some cases, I have had students drill the exact same problem 5, 6, 7 or more times. He learns more each time he works through that same problem. Be sure to cover up all his earlier attempts. Let him know this:  “Each time you drill that exact same problem, you must start right from the beginning as if you have never done it before.”

In extreme cases, to find out where the student is having trouble, I have the student tell me exactly what he is doing at each and every step in his solution procedure. In other words, he must verbalize precisely the part of the solution method he is performing at the moment he is performing that part. You will sometimes hear him say things that are not true. For example, if he is doing long division, when his is supposed to be dividing the divisor into the dividend he might say, “I am now multiplying” or “I am adding” rather than “I am now dividing.” Such mistakes can then corrected by the teacher. The result of this drilling procedure is a student who can solve his problems correctly without hesitation, wobble, or confusion.

Here is an example of guiding the student to solve his problem by the book. The principles involved in solving this simple problem apply equally to solving very complex problems in engineering, advanced math, physics, chemistry and other math-intensive subjects.

 

 

 

FOURTH AND FIFTH GRADE:
FINDING EQUIVALENT FRACTIONS

In the 4th and 5th grades, math students learn to find equivalent fractions by multiplying or dividing the numerators and denominators of common fractions by another fraction which is equal to one – equal to one because the numerator and denominator of the second fraction are the same number (and any number divided by itself equals one.)

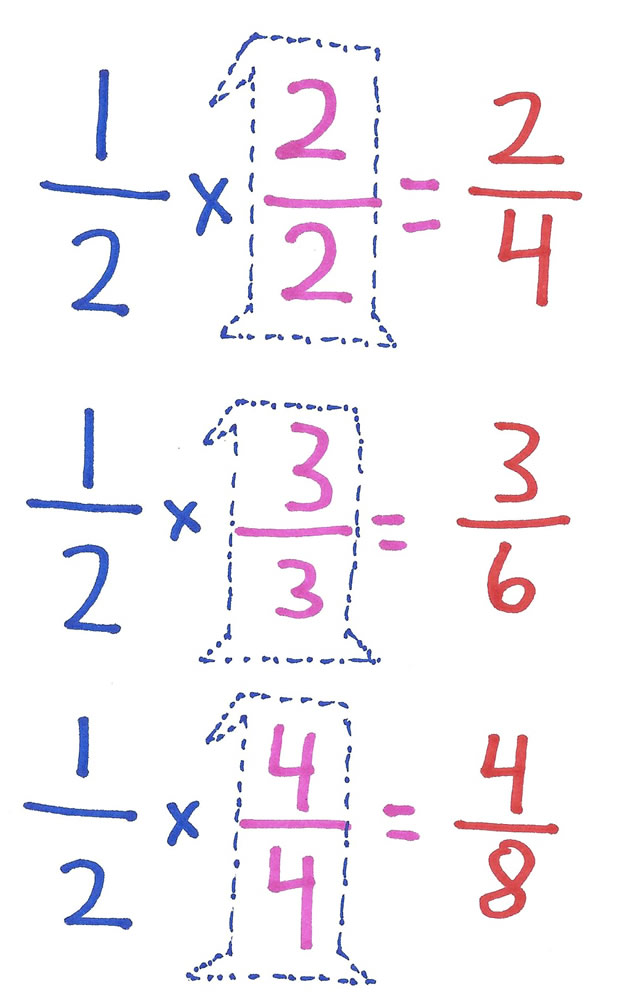
Here is a problem with the textbook’s solution method used to teach this principle.

 

 

Later, in Algebra, this simple process (multiplying or dividing the top and bottom terms of a common fraction by the same number to make an equivalent fraction) becomes one of the most powerful and versatile of all the algebraic tools used to simplify expressions and solve equations. (In Algebra, this tool is called the “fundamental theorem”, or the “fundamental law of fractions” or the “numerator-denominator same-quantity rule”:

THE NUMERATOR AND DENOMINATOR OF A FRACTION MAY BE MULTIPLIED OR DIVIDED BY THE SAME NONZERO QUANTITY WITHOUT CHANGING THE VALUE OF THE FRACTION.

However, when 4th and 5th grade students first become acquainted with this theorem, they do not know its purpose, value and importance and often neglect to follow this important procedure. Instead, using mental math, they write only the equivalent fraction and omit THE FRACTION EQUAL TO ONE.

 

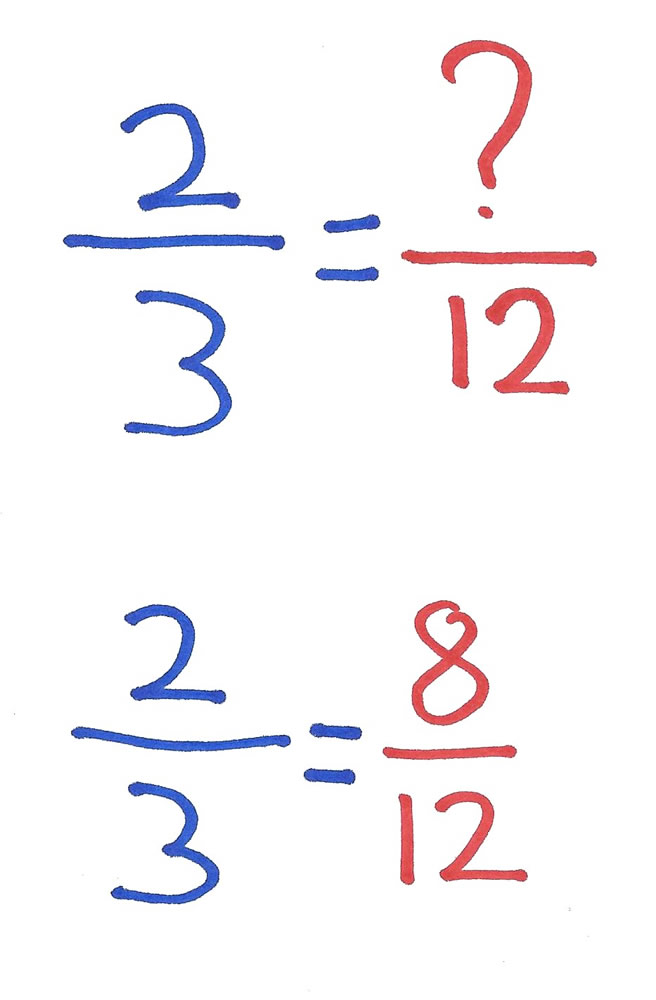
While it is both desirable and admirable that their mental math allows them to quickly find the necessary equivalent fractions, they have made a shortcut too soon. Shortcuts come later, AFTER they have mastered the book’s complete algorithm.

In Algebra and higher math, when they begin solving more complex problems, they will frequently need to know how to state in writing every step of the solution, including showing the actual multipliers – which can be a variety of constants, variables, monomial, binomials, trinomials, etc. — in order to stay on track.

Here an example of how this theorem will be used when simplifying a more advanced algebraic expression. The “FRACTION EQUAL TO ONE” (circled in red) is no longer the single digit from fourth or fifth grade but has become a binomial   with a variable term (X) and a constant term (2).

 

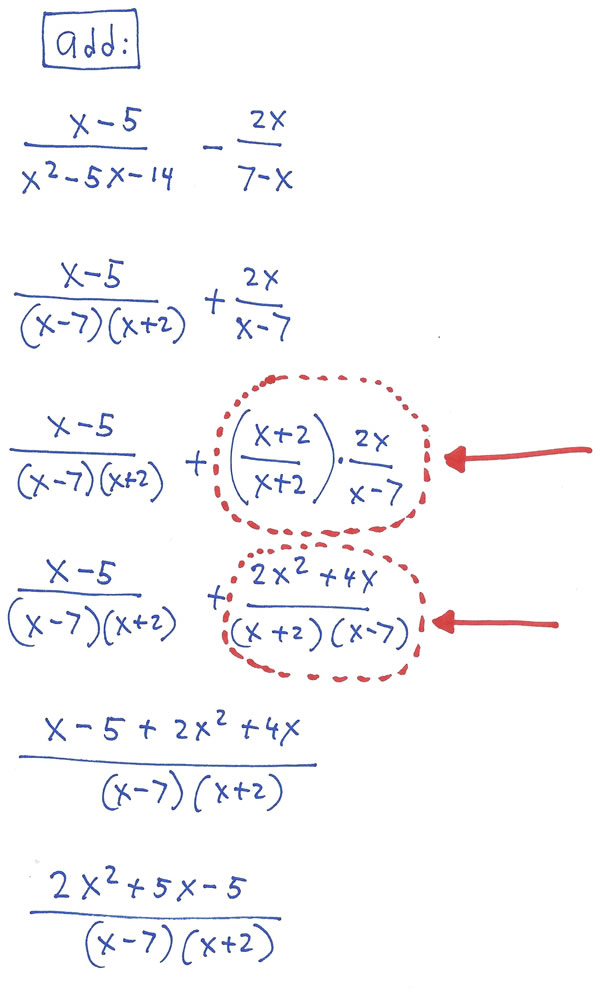
Therefore, in 4th and 5th grade, they learn to write down the full procedure until it is second nature.

Once they have learned to write it all out, they will, of course, drop out the procedure and just write the equivalent fraction. But by then the lesson is learned adequately and they will be far more likely to apply it properly in Pre-Algebra and Algebra when their 4th grade rule is transformed into the fundamental theorem of fractions.