The Other Side of Math
∞ PART FIVE ∞
HOW TO APPLY PROBLEM CREATION
 PREREQUISITE: OSOM STEP ONE
PREREQUISITE: OSOM STEP ONE
STUDENT SUCCESSFULLY COMPLETES
HIS CURRENT MATH TOPIC

The Number One Wins!
OSOM is not a substitute for the student’s current math course. Good, workable math textbooks and videos delivered to students by excellent teachers using effective study methods are the 24-carat gold standard. These are the texts (including video courses), these are the teachers and these are the study methods that teach the current theories, axioms, definitions, solutions, and rules which allow the student to master the fundamentals of the subject. OSOM Step 2 begins at the top of the student’s current math text. These new steps then go up in the direction of greater independent initiative and creativity. A student who is uncertain, confused or upset by his standard math curriculum cannot succeed when additional math ideas and procedures are piled upon a shaky foundation.
But once the student has mastered his books concepts, procedures, and problems it is time to move on and UP. Fixating a student’s attention on a textbook’s range of problems is always limiting. The usual text has many thousands of professionally designed problems which appear to cover every possible aspect of the subject. Whether one is studying Arithmetic, Pre-Algebra, Algebra, Geometry, Trigonometry, Pre-Calculus, or Calculus, the super-abundance and high quality of the text’s problems seem to leave no room or need for the student to create anything on his own. Thus, since the usual textbook does not require extensive problem creation, the student becomes a bystander to the creation of problems whereas he desperately needs to become the creator of problems.
 OSOM STEP 2
OSOM STEP 2
CLIMBING OUT OF THE BOX
DEMONSTRATIONS OF
THE PRACTICE OF PROBLEM CREATION IN MATHEMATICS
My observation: The process of producing self-created math problems is good for human beings. Conversely, using 99+% other-created problems for 12 years degrades the individual a little or a lot.
As soon as he knows with certainty the contents of the box, he can start climbing out. This section, “Climbing Out of the Box: Demonstrations of the Theory and Practice of Problem Creation” presents a few examples of actually applying Problem Creation. You will see that it is not difficult to do. In fact, if the student has truly mastered the topic as described in his book, Problem Creation is easy – a bit like falling off a log.
Remember, 1250 to 1750 is a conservative estimate of the quantity of separate, major topics a typical curriculum will cover from 1st to 12th grades. The topics I have chosen to demonstrate problem creation, solving and checking in this book could easily have been an entirely different selection of math problems. My choices do not mean that these topics are more important than other topics. Also, the grade where these topics are taught might be different in the curriculums of some schools.
I have applied Problem Creation to some of the following topics in actual tutoring sessions. Other examples are merely topics I am personally interested in. There are LOTS of math topics to choose from – hundreds and hundreds between first and twelfth grades!
 THE CREATION OF MATH PROBLEMS
THE CREATION OF MATH PROBLEMS
I usually tell the student that he is now going to make up his own problems without help from me or his book. This helps him to realize that he is taking an independent step.
There may be times with a particular student when it is better to not inform him something special is happening. In that case, I just close the book and tell him to make up a problem on the topic he is learning.
And some students may generally do a better job of creating problems if they are simply told to make up a problem on the topic being learned.
At first he may need to refer to his book to guide himself through each step of making up problems, solving the problems and checking the solutions to ensure that they are similar to the book’s problems.
Then perhaps he still uses the book but only a little, just enough to remind himself of the correct direction to take for his own problem-creation activity.
Now and then you will have to shift back to the book to re-orient the student and that’s fine
While the student is in the midst of making up, solving and checking his own problems, you will sometimes find he simply does not understand some aspect of that topic or an earlier topic. That confusion, of course, must be cleared up before continuing.
But eventually that book should be closed and he should be on his own. The mathematical ideas must come from him: his own memory, experience and creativity. While many are able to do this easily – in, literally, seconds or a few minutes – others may require considerable help from their teachers and even one-on-one work with tutors.
 GIVE THE STUDENT WINS
GIVE THE STUDENT WINS
It is my opinion that ALL STUDENTS HAVE THE POTENTIAL TO USE PROBLEM CREATION SUCCESSFULLY IF THEY RECEIVE HIGH QUALITY TEACHING AND STUDY ASSISTANCE.
Though I believe that the above statement is true (that, given adequate assistance, they can all do it), every teacher knows that students are dramatically unequal in their potential for understanding. Therefore, a good teacher does not expect the same speed and depth of comprehension from every student.
In the examples of Problem Creation that follow, please take careful notice that for some topics (fourth grade, “Equal Groups Word Problems”, and seventh grade, “Percent Word Problems”) I have asked the student for two distinctly different levels of problems. The first level of problem is for an “average student” (average in his personal interest in math as a subject, average in his speed of progress, average in his depth of understanding of math, etc.). The second level of problem creation is for a “math kid” – someone who is fascinated with mathematics as a subject and who travels at near-light-speed though his lessons, inhaling the concepts, procedures and rules and applying them correctly.
AS AN OSOM TEACHER OF PROBLEM CREATION, THERE IS NO SUBSTITUTE FOR KNOWING YOUR STUDENTS. BECAUSE YOU WANT THEM TO WIN, YOU ONLY ASK FOR PROBLEMS THAT THE STUDENT IN FRONT OF YOU HAS THE POTENTIAL TO CREATE.
 WHEN YOU ASK FOR TOO MUCH…
WHEN YOU ASK FOR TOO MUCH…
If you aim too high, you will know it. Recognize that you have asked him for too much, have aimed a bit (or a lot) too high and gracefully back down a level (or two or three or…) until you find the level of Problem Creation where your student can have his mathematical victories.
I sometimes aim too high. I have learned the hard way not to wait until my student is a sad puddle on the floor of my office. I immediately knock off (STOP) doing what I was doing that was too difficult. Then I honestly admit my error (mea culpa!) and aim for the right level of problem. If you were a little birdie on my shoulder, you might hear this:
“Oh, gosh, my mistake! I just gave you a higher level geometry problem. The problem I just asked you for — to find the area of an isosceles triangle with a base whose measure is a radical expression — it’s one or two steps beyond where you are now in your book.
“I have a better idea. Let’s go to the correct step. Don’t you agree? Oh, good! So, how about if you draw an isosceles triangle. Now that’s a nice isosceles triangle. You choose the lengths of the sides and the base. Exactly. How about if you make the measure of the base an even whole number? Yes, right on! Like 8 or 14 or… No, don’t use my numbers. Use your own. Good. And now make the two equal sides have another whole number measure. Perfect. In fact I couldn’t do better myself. See, look at the way you just drew that perpendicular bisector to the base from the vertex without me saying anything. Yes, I am glad you know how to do this.
“Now, how will you find the height. Hey, you said it! With the Pythagorean Theorem! Now go ahead and calculate that height. Cool math! Now calculate the area. Right on. Aha! Much better!”
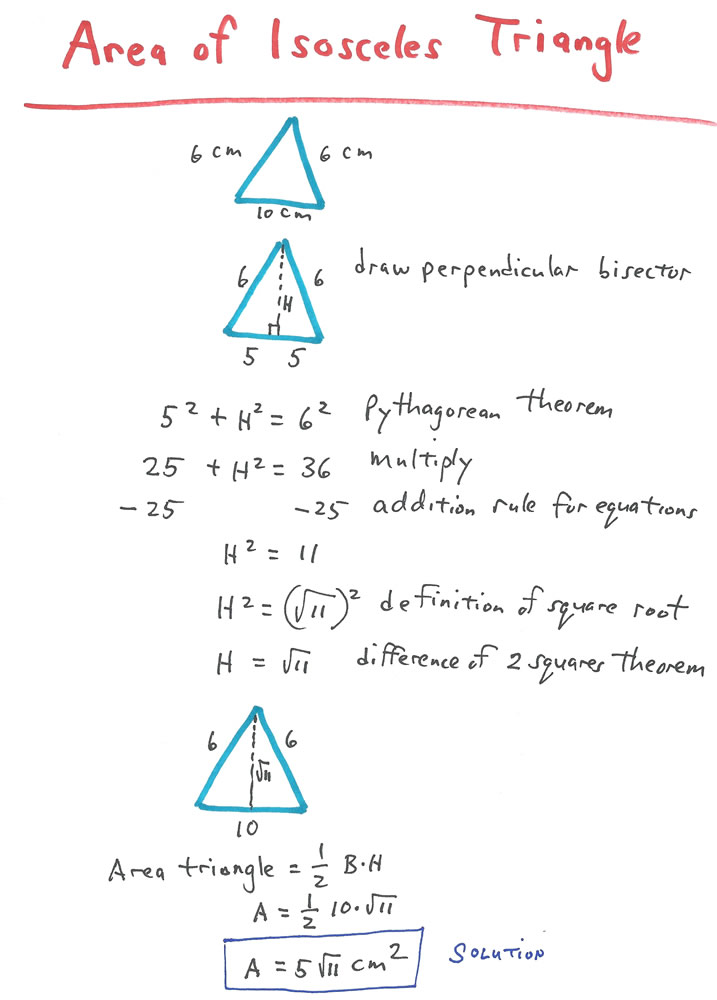
“Now, cover up the drawing you just made, then draw and solve that very same problem again until it is easy.
“Lovely math, Josh. Hmm, maybe you could make up another problem just like this one, but with different measures and all on your own? Easy numbers, please. Just like the book’s problems – no radicals or fractions in the base. Only even whole number bases and sides. You could? Great. Go for it.”
Naturally, having rescued my student (and myself) from the brink of mathematical disaster, I feel relief.
 TIMES WHEN I DO NOT USE PROBLEM CREATION
TIMES WHEN I DO NOT USE PROBLEM CREATION
As mentioned earlier, I have delivered approximately 10,000 sessions of math tutoring during the last 16+ years. In all that time, there have been very few individual instances of young people, perhaps 5 to 10, who I could not advance up from a level of mastery of a particular current math topic to the point where they could successfully apply Problem Creation to that topic.
I consider myself a competent, professional tutor, but the truth is that I am not a perfect tutor. Now and then I make mistakes while giving study assistance to students, mistakes in attitude and manner as well as math technique mistakes. Therefore, it is not unreasonable to suppose that a better tutor could have helped these few kids to really master their current math topic, after which they might have succeeded in applying Problem Creation to even complex Algebra problems.
 REPETITION
REPETITION
When a student demonstrates uncertainty while creating his problems, you have him create the same, exact problem again on a clean sheet with the first problem out of sight. When he can make, solve and check the same, exact problem without confusion or hesitation, only then do you have him create, solve and check another problem like the first one but with different numbers. And, if needed, another one and another one, etc., because we want him inventing problems with ease.
 MY WAY OR YOUR WAY?
MY WAY OR YOUR WAY?
The following problem creation examples were chosen by me based on the math curriculum I am using, my own experience as a tutor and the math that I find interesting. A few examples are accompanied by conversation I might have with my students, the words based on the words I would be likely to use with my students. However, I am not prescribing problems and I am not prescribing conversation that you must use. You are you. Communicate your own way. I would not be doing a good job if other tutors and teachers sounded like me.
Further, I am not even prescribing the specifications for the problem. For example, I might have a fourth grade student – if he is not a “math kid” – invent just one equal groups division word problem (missing factor). When he is successful with that creation, I might have him invent a single equal groups multiplication word problem (missing product).
But for a “math kid” I would probably use the same three numbers for all 3 equal groups (multiplication and division) problems. That’s my preference because it makes sense to me as a teaching method. My preference might not make sense to you based on your experience; in which case you might (possibly) have the student use three completely different sets of numbers and three completely different word problem situations. Or…
You are you. You have to find your own way of achieving the goal.
 Example One
Example One
PROBLEM CREATION IN FIRST GRADE:
WRITING ADDITION FACTS

I take it very easy and very lightly with first graders. If I am in doubt about their maturity and abilities, I back off and try again some days or even weeks later when they are more likely to have advanced mathematically beyond the level of kindergarten math. They cannot be sitting in a first grade classroom with first grade math in front of them while actually still attempting to master kindergarten math. In other words, first graders must be successful in doing first grade math before I add problem creation into their learning process.
“You just solved all those addition facts, all the way up to 9 + 9 = 18! And you got the right answers, too. Now, watch me. I’m closing your book. What did I do? That’s right, I closed your book. Let’s see you write down an addition fact like the ones you just solved in the book. Oh, you know you can do that? Good, I think you can, too. OK, pick up your pencil and get ready to write. No, I can’t tell you what to do. You have to chose the numbers of your addition fact. It’s up to you. Are you ready?”
Student quickly and correctly writes an addition fact. He uses counters to get the sum, which is expected during the early part of first grade.

He must write the whole fact correctly, digits lined up in the ones’ and tens’ places, the plus sign written to the left of the bottom addend and the answer sign directly under the addends. Don’t discount the importance of teaching them to write their facts correctly right from the start. When they learn to do it the right way first, it saves much time later when you might have to undo ingrained bad math habits.
“Great! Now write some more addition facts.”

“Nice add facts! Now take some of these pennies and show me what the 5 means. Good. Now use these pennies to show me what the number 7 means. Now show me the sum using pennies.”
Note that I used the word “sum” because he has just learned it in his lesson. If he looks blank when I say “sum”, then I have to help him understand that technical word.
“Hey, you did it! Good job! (followed by a loud “high five”, of course)
“Do you ever buy things at the store with your mom? You do? How could you use this 5 + 7 = 12 fact at the store?” If he does not know, we will play store, buying and selling actual toys, dolls, and stuffed animals. (Yes, I cover my desk with real things! I then arrange the prices so that one item costs five cents, another costs seven cents and the sum is twelve cents.
 Example Two
Example Two
PROBLEM CREATION IN SECOND GRADE:
MAKING FACT FAMILIES
“I can see you really understand these fact families. Can you make up a whole fact family by yourself? You can? Good. Book closed. Let’s start by you choosing the three numbers in your fact family.”
Student writes the numerals 4, 9 and 13 at the top of a blank page.
“Yeah, good start. Now write out the four facts in that fact family [two addition facts and two subtraction facts]. You want to use markers? How ‘bout if you start with a pencil. If you do this first fact family – all four facts – without mistakes, you can use markers for the next fact family. Deal?”
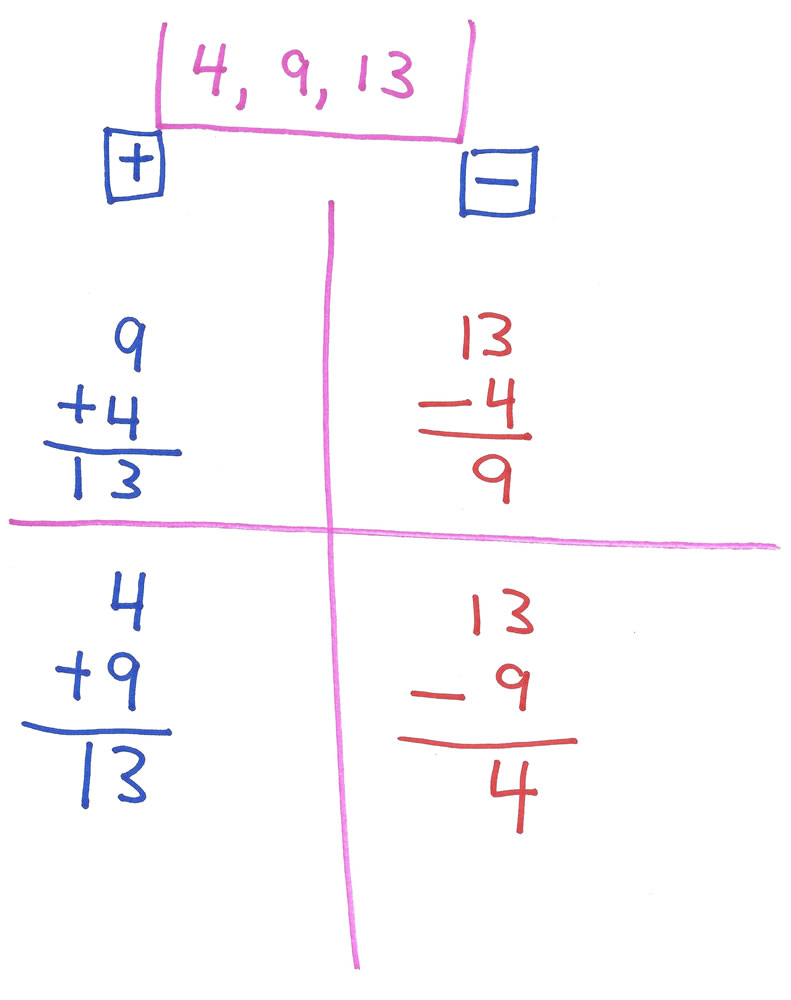
And when he has accomplished that task, you should ensure he understands what he has just done.
“Can you can point out the differences in the subtraction facts? Right on. And can you point out the sums in the add facts? Good job. Now, where are the addends? And the answer signs? Correct. And why did you choose 4, 9 and 13? Perfect”
“Now make up a story for one of the facts. Like, what could the numbers for this addition fact show? (I point to 9 + 4 = 13.) Candies? Presents? Friends? Money? You choose. No, your story doesn’t have to true. Just make it up. You can even lie! Like, imagine it.”
 Example Three
Example Three
PROBLEM CREATION IN THIRD GRADE:
SUBTRACTING ACROSS THREE ZERO’S
“You’ve just learned to subtract across three zero’s by borrowing from the thousand’s place. Let’s see if you can make up a similar problem on your own without using the book. (I close the book.) Write out a subtraction problem where you have to subtract across three zero’s. You have to borrow from the thousand’s place in order to subtract in the one’s, ten’s and hundred’s places.”
“Good problem. Now solve it.
“Good. Now check it.”

“Now demonstrate your subtraction problem and its difference (answer) with these place-value pieces (manipulatives) representing one, tens, hundreds, and thousands. Be sure to show the regrouping.
Note: I definitely do use math terms the students has already learned, terms like “difference”, “place-value” and “regrouping.” In other words, I “talk math” to the kids when it is appropriate, because part of “learning math” is becoming familiar with “talking math.” This gives me the opportunity to find out what they don’t understand or have forgotten. For example, if a student gives me a horribly confused look when I say “place-value”, I know he doesn’t understand the term “place value”. Even though he passed his examinations on place value in first grade, second grade and third grade, I still must take immediate steps to remedy that confusion before continuing with Problem Creation.
“When would you need to solve a problem like this in your life?”
If he has no clue (a common occurrence) how this subtraction algorithm might apply to a real-life, I help him with this, too. Best is to have a bunch of dolls, animals, spaceships, racing cars, etc., and real money and make up a whole buying/selling situation right on the desk. It works!
 Example Four
Example Four
PROBLEM CREATION IN FOURTH GRADE:
EQUAL GROUPS WORD PROBLEMS
In Arithmetic, “Equal Groups Word Problems” are word problems that involve multiplication or division. The central concept of the lesson is that division finds missing factors and multiplication finds missing products.
For an average student, I might just ask for an equal groups word problem that is solved by multiplication. The student writes his word problem:
“Each package has 8 pencils. There are 7 packages. How many pencils are there in all?”
Then the student solves the problem and, finally, checks his answer:

I would probably follow that by asking for an equal groups word problem that is solved by division:
“Bob put 6 tennis balls in each can. He has 42 tennis balls in all. How many cans does he use?”
The student then solves his problem and checks his answer:

Now let’s see what Step 2 might look like if I am helping a “math kid” (advanced student) who I personally know is eager for an intellectual challenge, who genuinely enjoys math and who would be seriously disappointed if I did not push him as high as possible. I might ask him to make up three different equal groups (multiplication and division) word problems but each of the three problems must use the same three numbers – the same two factors and the same product.
Since this is rather complex, I would probably write out my specifications in simple words.
I ask him to plan his three problems carefully. I know he must choose one multiplication fact as the basis for all his calculations so there will be no remainders. I give him some help on this if needed, referring him back to the text when appropriate.
I know that in each of his three problems, a different number must be missing:
► When the “how many in all” (the product) is missing, you have a multiplication pattern.
► When the “how many in each group” (the top factor) is missing, you have a division pattern.
► When the “how many groups” (the bottom factor) is missing, you also have a division pattern.
I let the student work his own way through this more challenging problem. He tries a few multiplication facts and finally settles upon his three numbers: two factors and their product based on one multiplication fact: 5 X 12 = 60.
For this creation, the student chooses goats and pens. With me just guiding him slightly when he dives off the correct line of reasoning, after some erasing and fumbling, he comes up with the following three perfect problems and solutions.
First he writes out the 3 numbers and what each number means.
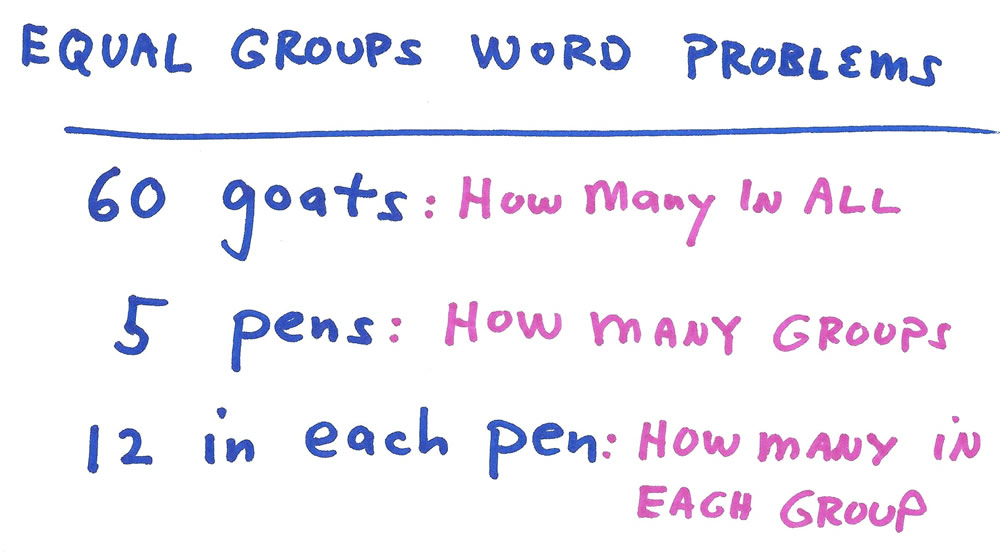
Then he writes out his first (of three) word problems:
“There are 5 pens and 12 goats in each pen. How many goats are there in all?”
The product, the “How many in all?” is missing, so this is a multiplication problem.

Then he writes out the second of his three word problems:
“There are 60 goats in all. There are 5 pens. If each pen has the same number of goats, how many goats live in each pen?”
The top factor, the “How many in each group?” is missing, so this means division:

Here’s the third (and last) of his three equal groups word problems:
“There are 60 goats in all. There are 12 goats in each pen. How many pens do you need?” The bottom factor, the “How many in groups?” is missing, so this is a division problem.

Let’s suppose this student showed definite uncertainty while writing his three problems, hesitating over and over, erasing this or that and asking nervous questions. When he was done, I would have him place the above problems and numbers out of sight and do the exact same three problems (same numbers, same everything) again (and again) until he was really fluent making them.
Then (because he showed numerous uncertainties), I might ask him to write another set of three equal groups problems based on a different multiplication factor, perhaps involving different animals (like chickens) and different kinds of groups (like chicken coops) appropriate to those animals. Naturally, he decides which animals and which groups. (Or he might just branch off to apples and bags or…!) This time he would probably need no help and would create his problems with ease.
If he was still showing uncertainty or confusion, I would go right back to his book to find out what he missed before continuing. He must end with certainty in his ability to create math problems for this topic.
 Example Five
Example Five
PROBLEM CREATION IN FIFTH/SIXTH GRADE:
GRAPHING RECTANGULAR COORDINATES
To create and solve this problem the easy way, the student uses ready-made graph paper. Using only his knowledge and skill with coordinates and quadrants, he creates and graphs his own ordered pairs. Or (harder, but lots more fun and producing lots more learning) he can, if he chooses, draw the entire Cartesian system using a ruler and a pencil and end up graphing his chosen ordered pairs accurately on his own graph paper as the last step.
To start, I have him create five ordered pairs of rectangular coordinates and graph them on graph paper. At least one point must be located in each of the four quadrants.

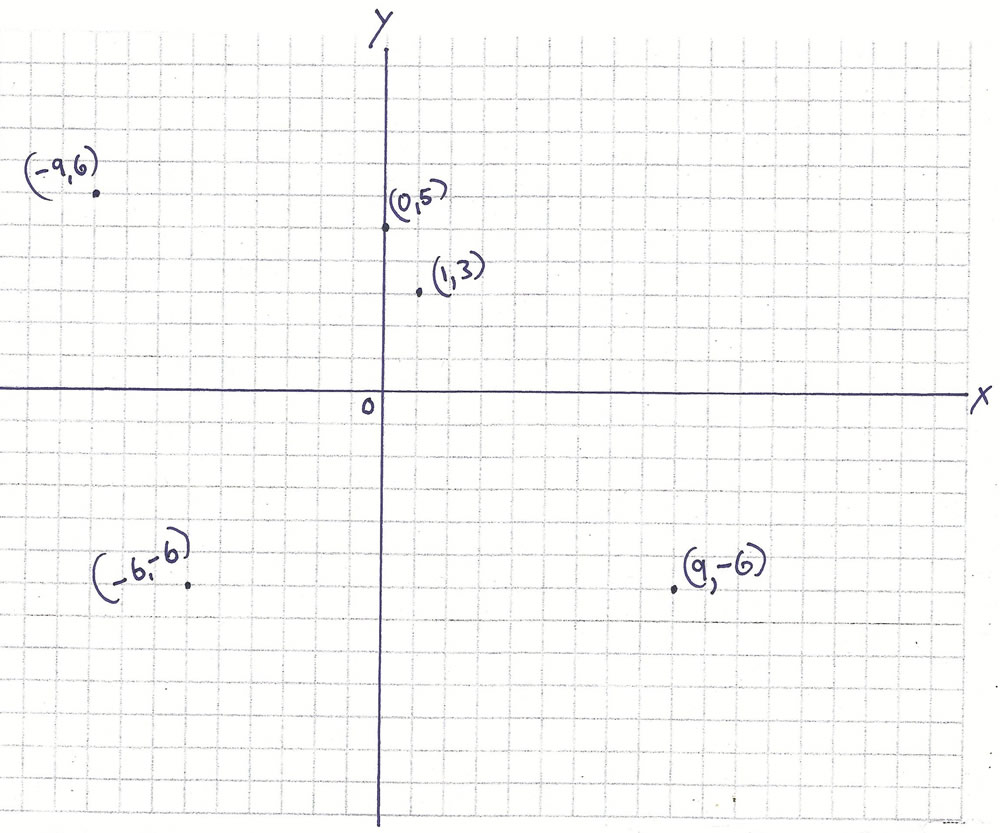
 Example Six
Example Six
PROBLEM CREATION IN FIFTH/SIXTH GRADE:
WRITING AND SAYING DECIMAL NUMBERS
Using standard notation, he must write three decimal numbers. Two of them must have 4 decimal places (ten-thousandths) and one must have 5 decimal places (hundred-thousandths). One of the decimal numbers cannot have any whole number digits. After he has written out his decimal numbers using standard notation, he then translates them from numerals to words.

Because the ability to read such numbers is extremely useful, after he writes the decimal numbers, he should practice reading them aloud until he can say them flawlessly.
 Example Seven
Example Seven
PROBLEM CREATION IN SIXTH GRADE:
MULTIPLYING AND DIVIDING SIGNED NUMBERS
For most students, I might have them create simple signed number problems which are solved by multiplication.
![]()
When they can do that easily and many times with different numbers, then I might have them create signed number problems that are solved by division.
![]()
When they can do both exercises fluently with different numbers and different combinations of positive numbers and negative numbers they have got it.
For a “math kid”, I might ask him to demonstrate all four possible combinations of signed numbers (positive-positive, positive-negative, negative-positive, and negative- negative) when multiplying the same two numbers.
When he has accomplished that, the student could demonstrate all four possible combinations of signed numbers (positive-positive, positive-negative, negative-positive, and negative- negative) when dividing the same two numbers. This not easy and I would not ask this of many students.

 Example Eight
Example Eight
PROBLEM CREATION IN SEVENTH GRADE:
PERCENT WORD PROBLEMS
To ease the way into the process of problem creation, it might be necessary for you to write out the specifications of the problem you want the student to create with. He can refer back to your specs. Naturally, such instructions should always be written at his level of reading skills.
For the great majority of students, I would only ask them to create a percent word problem using same the procedure given in their textbook.
The student writes out his word problem:
“Fifty girls went to the party. Forty percent of them wore dresses. The rest wore pants. How many wore dresses and how many wore pants? What percentage wore pants?”
He then translates it to an equation, solves and checks the solution:

In the above example, the student chose the final number as the unknown. He could have chosen the percent as the unknown or the original amount as the unknown. After he has accomplished the above on his own, you might ask him to create another percent word problem and specify which of the three values you want to be the unknown: percent, original amount, or the final number.
 Example Nine
Example Nine
PROBLEM CREATION IN PRE-ALGEBRA:
THE ADDITION RULE FOR EQUATIONS
IF THE SAME NUMBER IS ADDED TO BOTH SIDES OF AN EQUATION, THE SOLUTION SET IS NOT CHANGED.
Here’s an example of applying Problem Creation with an Algebra student who is learning a vital topic: the addition rule for equations.
This student has been successful in applying the addition rule for equations to the book’s problems. With the book open, he can solve problems like:

Solving these problems requires a new way of thinking: algebraic addition. The student appears to understand the idea of adding the same number algebraically to both sides of an equation to isolate the variable on one side of the equals sign.
I write down the easiest of the above problems and show it to him:
x + 5 = 14
“Make up a problem like this one. Use a different numeral for the constant and a different letter for the variable but keep the same pattern.”
He writes his own equation perfectly per my instructions:
x – 163 = 114
“Now solve the problem, writing out every step exactly the way you solved the book’s problems. No steps omitted. No mental math allowed.”
This he can’t do. Without the book open and Saxon’s clearly written solution in front of him, he cannot remember the procedure. He fumbles and stumbles and stops. Back we go to the book.
I test him to ensure he knows the rule addition rule for equations cold. He does.
I ask him questions to see if he knows why this rule is used. Why is it important? His answers show that he knows this oh-so-vital fundamental principle.
Aha! He simply doesn’t know the procedure well enough. That’s an easy fix: he needs hardcore drilling. With the book open, he drills solving each of the above four equations until he can do each one smoothly without referring to the book. In other words, he learns the steps by doing them over and over and over until he simply knows them with certainty.
Once, again, with the book closed, I ask him to solve his equation with all steps written clearly and no mental math. This time he does it flawlessly. He is working and thinking confidently.

By applying the same procedure, I get him to create, solve and check (by substituting his solution for the variable) each of the four kinds of equations listed above: one variable with a positive integer, one variable with a negative integer, one variable with a decimal fraction and one variable with a common fraction.
We discuss how this rule might actually be used in life. He has no clue. I give him some real life problems that could be solved by applying this algebra rule. He not only gets it but makes up his own situation and solves it using the addition rule for equations.
 Example Ten
Example Ten
PROBLEM CREATION IN GEOMETRY:
FINDING THE DIAGONAL OF A SQUARE
The student is asked to find the measure of the diagonal of a square whose sides measure ____ inches. I tell him that the measurement of the sides should be small enough so that he can easily check his math by constructing an actual square, drawing the diagonal and checking his algebraic calculations with a ruler. (See Part 8, Checking Answers, where this same problem is used to illustrate checking answers to Geometry problems.)


 Example Eleven
Example Eleven
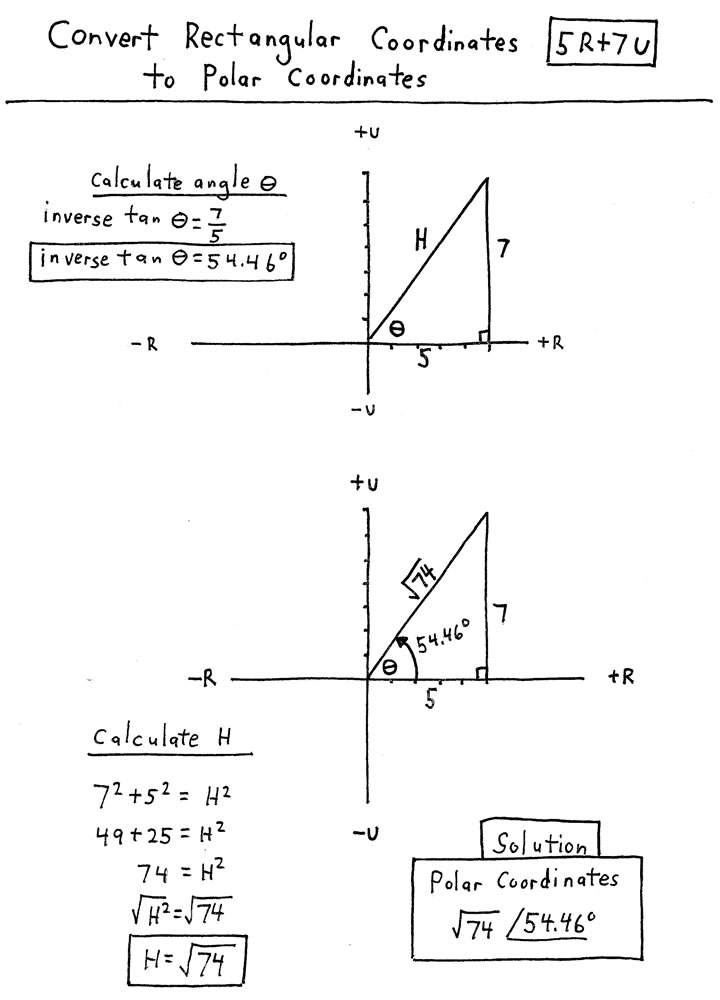
PROBLEM CREATION IN TRIGONOMETRY:
CONVERTING RECTANGULAR COORDINATES
TO POLAR COORDINATES
The student is asked to choose an ordered pair of rectangular coordinates and convert those to polar coordinates. He must use the same procedure he has learned in his lesson. He must know a lot of math to handle this topic: basic trig functions, inverse trig functions, the Pythagorean Theorem and how to use it, graphing on a rectangular coordinate system, finding the square root of both sides of an equation, etc.
 Notes for Teachers
Notes for Teachers
For some students you are asking a lot when you ask them to create, solve and check problems of their own. For these boys and girls, you will need to walk them through the steps very slowly, with great care and gentleness. “Demanding” simply does not work in OSOM. I have tried “demanding” and it only results in unhappy kids. I cannot over-emphasize the need by teachers and tutors to be patient, tolerant and yet persistent on the OSOM Problem Creation step early in the process.
So, at the very beginning, whatever the age of the student when the student is just learning to use it, take it easy. Consider that you are treading within the intimate perimeter of your student’s own universe when you ask him to create these problems. When you put on your hat as an OSOM teacher, you must become more of an art teacher than a drill instructor because you are dealing with the creative process in individuals and this process is different for each.
Many boys and girls can do it with remarkable ease. When you ask such children to walk, they walk with perfect balance and poise. For others, at the beginning, it can be a shock, as you are requesting that they stand mathematically on their own, and they possibly have not been asked to do this before. “Coax”, I think, is the best action verb to orient a teacher’s or tutor’s manner and attitude.
After a while, when the student has experienced success creating problems for a number of topics, he himself will start thinking in the direction of “What problems can I create for ______?” when he is at the end of learning a topic.
Can this educational process be done as a group project with every student of a whole class at the same time or must it always be done on an individual basis?
I have never done it with a whole class, only with individual students. However, after a group of students has been trained on OSOM Step 2, I believe Problem Creation can be done with that particular group of students without teacher guidance beyond checking the result – though some students may always require a degree of individual attention to succeed in achieving the most desirable result.
 Giving Written Instructions
Giving Written Instructions
Some students will not be able to understand and act on your spoken instructions, but they will be able to duplicate and carry out written instructions. Thus, to further ease their way into the process of problem creation, it is sometimes necessary to write out the specifications of the problem you want the student to create so he can refer to your specs. Naturally, such instructions should always be written at his level of reading skills. And sometimes you must be right there with your physical finger pointing to your instructions. It takes what it takes!
I never ever touch kindergarten kids with this method.
I use it lightly with first graders, a lot more with second graders and tons in third grade.
Starting in third grade, you can just pour on the steam providing, of course, you use Problem Creation with understanding, kindness, good coaching and awareness of the actual abilities of the person in front of you.
Step Two, Problem Creation must not be done only at the end of the student’s current textbook. That is far too late; by then even more students will be a little or a lot less alive to the subject of math. Self-created problems are done immediately after each individual textbook topic is mastered. That means 125 or 150 or more separate major topics per course per year learned with genuine certainty by the application of OSOM Step Two, Problem Creation. Time permitting, have him create problems with the minor topics as well.
A student must be helped if he can’t create his own problems for any particular topic. Because when he really understands the theory, definitions, algorithms and solutions of a particular topic, he can create his own problems and solve them nicely.
The truth is that the math textbook’s problems merely skim the surface. With certainty, it is possible to systematically train students to create or pose their own problems, problems that cover all the major areas of math tech learned in their math texts, and then solve and check these self-created problems accompanied by gains in learning and skill far beyond that achieved by using the book alone.

