The Other Side of Math
∞ APPENDIX D ∞
PREVIEW OF OSOM STEP 6
EXTRAPOLATION, INVENTION & DISCOVERY
good ideas, better ideas, big ideas
 DEFINITIONS
DEFINITIONS
DEFINITION OF EXTRAPOLATION
EXTRAPOLATION IS THE ACTIVITY OF STARTING WITH KNOWN FACTS AND USING THESE KNOWN FACTS AS THE BASIS FOR DRAWING CONCLUSIONS AND MAKING GENERAL STATEMENTS ABOUT A SITUATION OR WHAT IS LIKELY TO HAPPEN IN THE FUTURE. KNOWN FACTS ARE THE STARTING POINT IN EXTRAPOLATION. CONCLUSIONS AND GENERAL STATEMENTS ARE DERIVED FROM THESE KNOWN FACTS.
DEFINITION OF INVENTION
INVENTION IS SIMPLY THE CREATION OF SOMETHING NEW.
DEFINITION OF DISCOVERY
DISCOVERY IS THE FACT OR PROCESS OF FINDING OUT ABOUT SOMETHING FOR THE FIRST TIME.
 THE PRODUCT OF STEP 6
THE PRODUCT OF STEP 6
One result of the OSOM program is an individual who is intimately familiar with the process and results of extrapolation, invention and discovery in the realm of science and mathematics. He can recognize the phenomena when he observes it, reads about it and hears about it coming from others. He can perceive it occurring in himself because he is familiar with his own peculiar, particular and unique modes of extrapolation, invention and discovery. Armed with that knowledge, he can increase its frequency of occurrence and accuracy of results as regards his own life and work.
 EXTRAPOLATING, INVENTING, AND DISCOVERING
EXTRAPOLATING, INVENTING, AND DISCOVERING
ARE INNATE HUMAN ACTIVITIES.
These three, high-level human abilities are innate. Reader, wherever you are at this very moment, look around you. Unless you live in an undeveloped area of countryside or wilderness, the results of human extrapolation, invention, and discovery are likely to be everywhere.
In children, these three abilities and drives are immensely powerful and operate almost non-stop. Kids are busy extrapolating, inventing and discovering things about themselves and the world they live in. But, later in life, due to the stresses of living in an imperfect world, these pro-survival, creative impulses can glow dimly indeed!
Some people clearly recognize that they do, in fact, extrapolate, invent and discover. Others carry out these vital actions without much awareness of what they are doing.
Since I tutor all subjects, not just math, I have observed that my math students do far less extrapolating, inventing and discovery in math than the same students do, for example, in reading and writing.
Well, how about me? Do I extrapolate, invent and discover things? Yes, definitely yes. Especially in the field of math education, I have ideas that are my own. Some of my ideas are useful only to me as an individual who is studying mathematics. Some ideas have also proved useful to the students I am tutoring and even to other teachers. Still other ideas have not proven their worth either to me or other people. These I discard — and then I get some new ideas!
 GETTING NEW IDEAS
GETTING NEW IDEAS
I intentionally get new ideas about math. I work hard at it because I have students who need help. The saying that “necessity is the mother of invention” is true. I think up new methods of teaching them math while tutoring, between tutoring sessions and at mealtime. I also get lots of new ideas while swimming hard laps (with fins and swim gloves at the YMCA), while communicating to my closest friends about my favorite subject (math) and even during sleep (which means I wake up with ideas, some of which I actually remember and later use.) While none of this may seem magical or earthshaking, it is a lot of fun and enriches my entire life.
Since I am the extrapolator, inventor and discoverer I know best, I will use my own experiences to preview examples for this step.
For starters, my entire math educator’s website (MathCreativity.com) is an example of OSOM STEP 6.
The examples that follow are a look at the ordinary, day-to-day extrapolations, inventions and discoveries of a single individual who is, himself, in the midst of doing the OSOM program – Bruce Silton.
THE EXAMPLES IN THIS APPENDIX ARE ONLY INTENDED TO CLARIFY WHAT STEP 6 MEANS TO ME. IT IS CERTAIN (and I do I mean CERTAIN) THAT STEP 6 WILL MEAN SOMETHING DIFFERENT TO YOU.
BIG NOTE: STEP 6 SHOULD BEGIN NOT AT THE UNDERGRADUATE, MASTERS, OR DOCTORAL LEVEL, BUT AS SOON AS THE STUDENT HAS COMPLETED OSOM STEP FIVE. THE YOUNGER WE START (WITHIN REASON) THE MORE CREATIVE MATHEMATICAL ACTIVITY AND PRODUCTS WE WILL GET. YOUNG PEOPLE ARE BUBBLING WITH NEW IDEAS. IF WE DIRECT THAT CREATIVENESS IN THE DIRECTION OF MATHEMATICS….


 AN EXAMPLE OF EXTRAPOLATION:
AN EXAMPLE OF EXTRAPOLATION:
Equivalent Fractions Chart
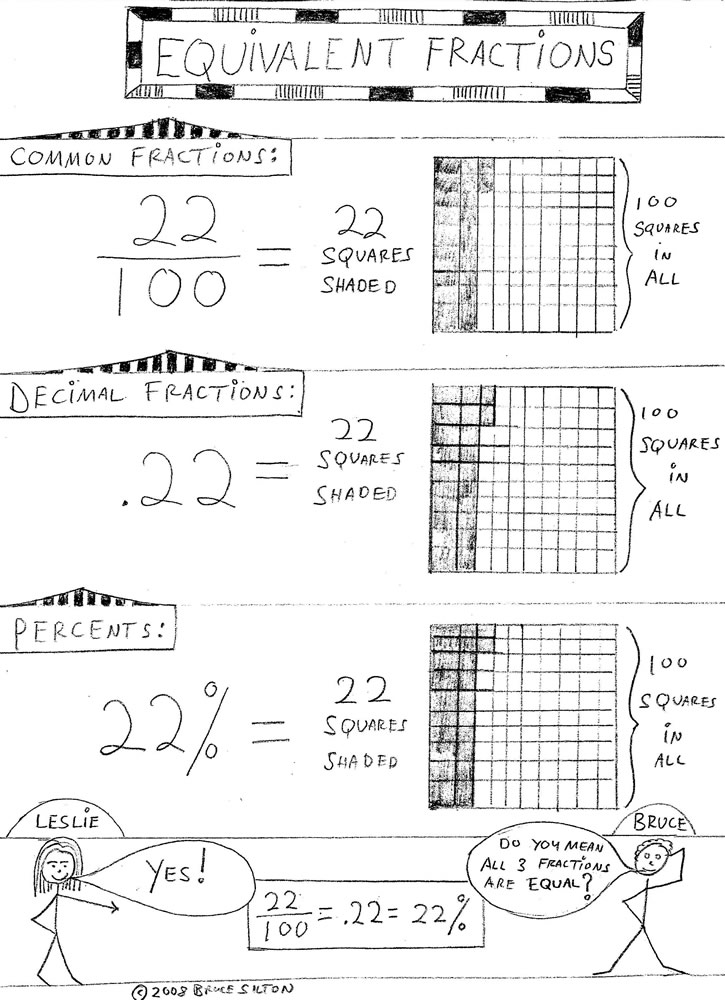
My Sister Leslie and I Discuss Equivalent Fractions
In 2008, I drew up a simple “equivalent fractions chart” based on the Saxon math textbooks used in our 4th, 5th and 6th grades. This chart helped me and my students to better understand the relationship between common fractions, decimal fractions and percents.
Years later, in 2016, intending to further improve the ease and speed of learning fractions, I developed a similar but more advanced chart called the “Family of Fractions, Numerator-Denominator Chart.” This new chart includes far more data in compact form. It has a new, more appropriate title: the “Family of Fractions”. It stresses the common elements of the three types of fractions: all have a numerator and a denominator. With this chart, a student can see at one glance the different ways that numerators and denominators are written in each of the three members of the fraction family.
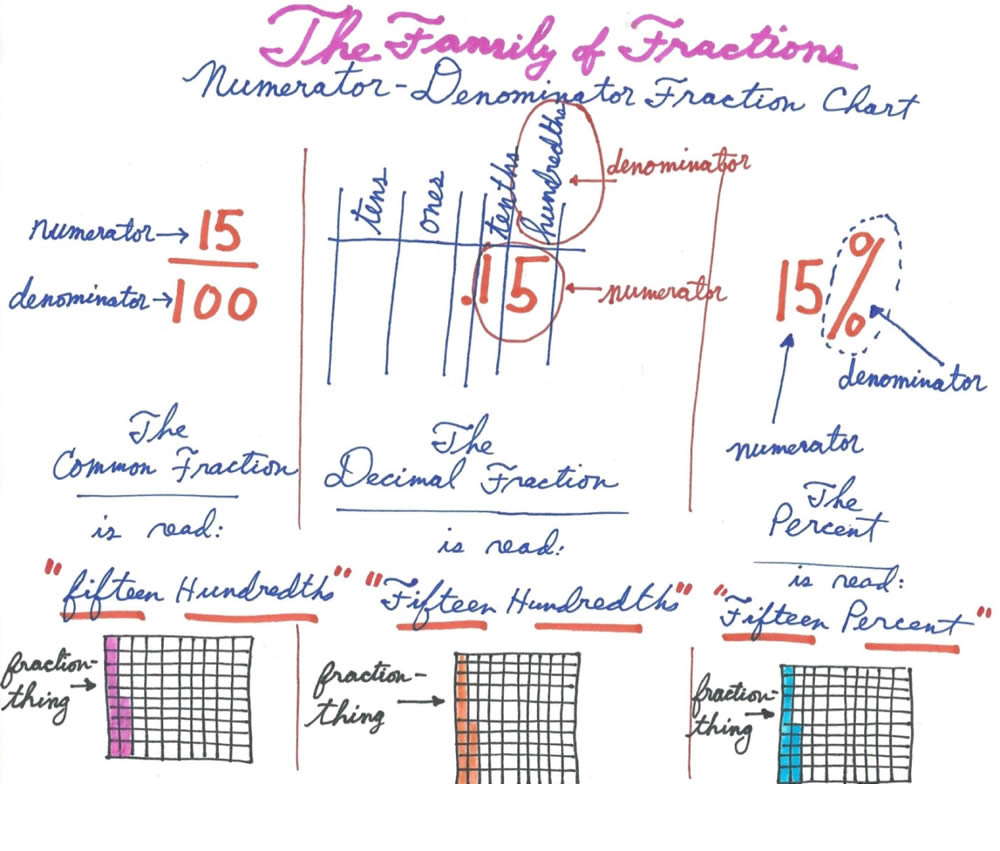
The above series of extrapolations based on data in Saxon math textbooks led to my having a greatly improved ability to teach fraction fundamentals.
(The chart also includes a genuine “discovery”: the “fraction-thing”, which is noted at the very bottom of the chart. I will describe the “fraction-thing” in the “Discovery” part of this Step 6 Preview.)
 ANOTHER EXAMPLE OF EXTRAPOLATION
ANOTHER EXAMPLE OF EXTRAPOLATION
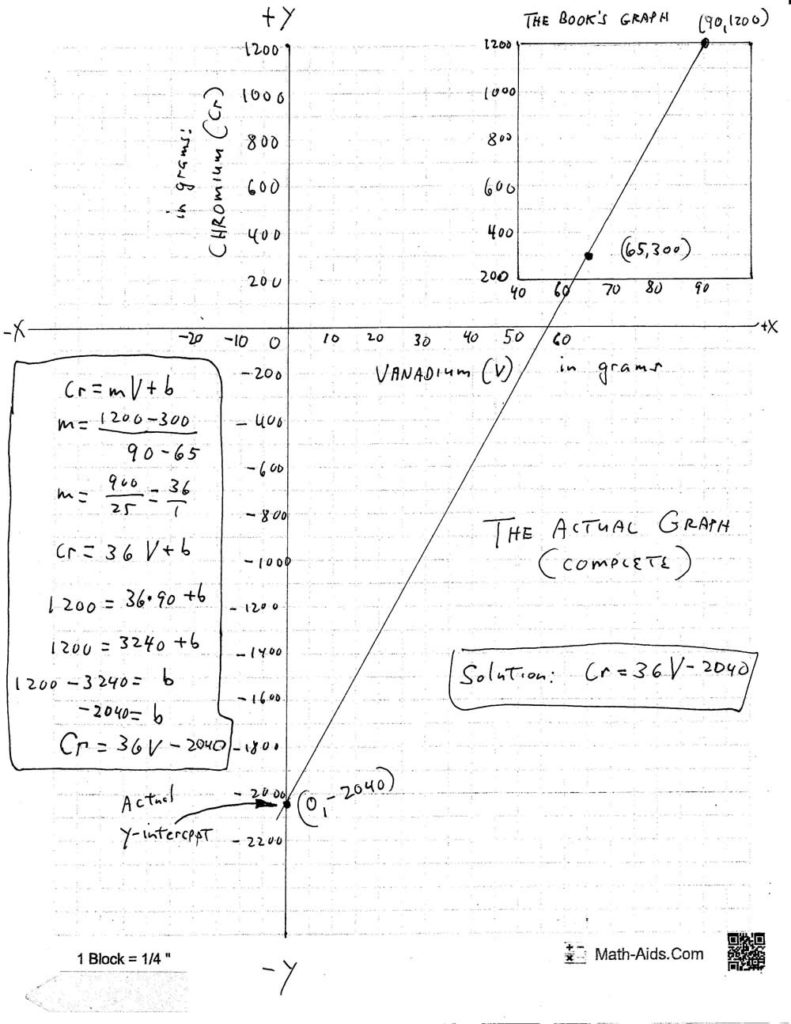
Extrapolation: Extending a Data Point Graph
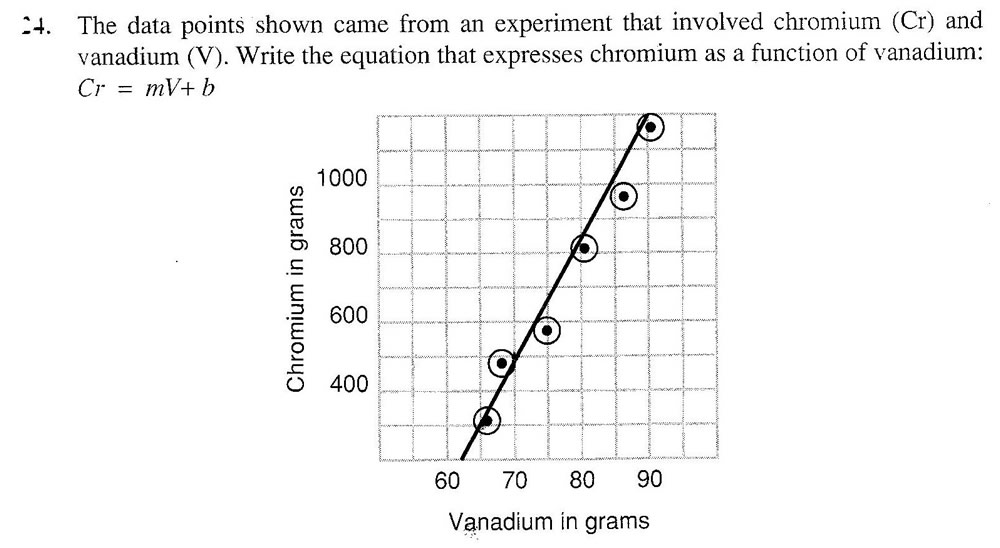
Next is an algebraic extrapolation made in an effort to better understand “data point graphs”, a topic from Algebra 2. A “data point” is a single piece of factual information derived from measurement or research. A “data point” can also be the mark on a graph that corresponds to a single piece of information derived from measurement or research. On the graph below, the points with the circles around them represent single measurements from such an experiment.
This extrapolation using data point graphs starts with a problem given in Lesson 69 of Saxon’s Algebra 2 textbook, Second Edition. The problem concerns graphing the results of a laboratory experiment involving two elements: chromium and vanadium, both metals that are used to make steel alloys harder than ordinary steel. Here’s the book’s statement of the problem and the book’s graph:
A letter I wrote to a colleague at school explains my extrapolation:
Feb 27, 2016
Dear ,
I found it difficult to understand the linear equations I was coming up with as solutions to experimental data point problems in Algebra 2 — even when my equations were correct. I hypothesized that my own confusion was caused by the “Incomplete” graphs in the book.(The book’s author is correctly saving space in his book because the complete data point graphs are far too big to use full size.)
So I experimented by extending some of the book’s graphs (only the graphs that are incomplete) to include enough of the actual graph so that the y-intercept, where X = 0 (which, after all, is the definition of a y-intercept) is also graphed.
It worked for me. After that, I had no problem understanding the book’s graphs or the stated problems or my own solution. In other words, I got correct solutions that made sense to me.
So, the whole point of the attached extended graphs is: If the partial (incomplete) graphs used in some experimental data point problems make it difficult for a student to understand the problems and the solutions, then the student can draw the complete graph so that the y-intercept occurs where X=0.
This helps me. Let me know if this is useful to you and your students.
Bruce
 AN EXAMPLE OF INVENTION:
AN EXAMPLE OF INVENTION:
“New Numbers with New Properties”
In June of 2016, while studying the Algebra 2 subject of imaginary and complex numbers, I learned that there had been a major controversy in the field of mathematics lasting hundreds of years surrounding the existence (or non-existence) and the value (or lack of value) of imaginary numbers ). This dispute was finally resolved in the 20th Century when it was discovered that imaginary numbers had important, real-world applications in electronics, engineering and physics. Because imaginary numbers were difficult for me to grasp, I used some evening and weekend time to research the subject. At the end of this project, I wrote a paper describing the results of my research — “The Future of Numbers” and subtitled, “Imaginary & Complex Numbers in the Real World.”
At the end of this paper I summarized my findings with a pure invention: a new category of numbers, a category that did not exist before I invented it.
“Given mankind’s documented history for discovering and/or creating new and useful mathematical tools that have provided us with greater and greater control of the physical universe, would it really be so surprising if current and future mathematical researchers, while attempting to uncover further hidden properties from the “measurable”, (the purely quantitative aspects of our universe) bring to light ‘New Numbers with New
Properties?’ ”
“I can therefore envision mathematicians, physicists and other scientists (both amateur and professional) uncovering NEW NUMBERS WITH NEW PROPERTIES that prove to be just as useful as the common series of numbers we call “real numbers” — and as useful as imaginary and complex numbers — and then applying these New Numbers with New Properties to achieve practical ends.
“In keeping with the possibility of new numbers being discovered or created, I propose designating those numbers that can be found somewhere or anywhere off the number line to be
NEW NUMBERS WITH NEW PROPERTIES.
“Such a name would, of course, be instantly abbreviated to just New Numbers and then further abbreviated to NN. (But even NN — italicized, of course — has a nice ring to it!)
“But without the number line, how do we orient ourselves with regards to New Numbers with New Properties?
“The answer is:
BY MEANS OF REAL-WORLD APPLICATIONS.
“The question “Where is New Number XYZ?” is answered by: How will NN XYZ be used? What practical purpose does it fulfill right now? Where do we start applying NN XYZ to the world of people, mountains and bees (and dirt-cheap, renewable sources of energy and black holes and faster-than-light starships and….”)
“If no current purpose can be found, we still do not discard, ridicule or smash New Number XYZ. We carefully and respectfully place it in a bin labeled:
THIS IS A VERY SPECIAL NUMBER BIN!
RESERVED FOR NEW NUMBERS WITH NEW PROPERTIES THAT HAVE NO IMMEDIATE APPLICATIONS. HOLD INDEFINITELY FOR MANKIND’S FUTURE.
“If such NEW NUMBERS WITH NEW PROPERTIES have an appropriate name and category to be part of, perhaps they will be warmly welcomed, validated and more rapidly applied to helping mankind increase its survival rather than becoming the subject of just another sad event in that dull series of jealousies, arguments and wasteful controversies that have occasionally marred the history of scientific advance.”
 AN EXAMPLE OF DISCOVERY:
AN EXAMPLE OF DISCOVERY:
The Fraction-Thing
The (short) story is this: Way back in 2007, many of my students were confusing the physical universe object that a math fraction represents (the actual thing, like a cake or a pie, separated into equal parts) with the math fraction itself (the number). Per definition, a mathematical fraction is only a number: 1/4 or .25 or 25%. But my students — one for one — would point to a picture of a pie or a cake separated into equal parts to show me what a math fraction was. And, of course, things are not numbers. Numbers represent things; numbers are just symbols for “how many things.”
A survey of some 2O dictionaries brought to light this fact: there was no name for the thing that math fractions represent. By accident, I had come upon an unnamed entity in math, and its lack of a name was causing my students considerable confusion when trying to master fractions.
So, I gave this unnamed thing a name: “real-thing fraction”. My initial idea of the “real-thing fraction” was a bit off the mark. Let’s look at this sketch done in 2008. Note the arrow. It points to a single equal part (one candy) from a box of four candies. I mistakenly named that one equal part as “the real-thing fraction.” This is not true. Actually, the entire box of candies with its four equal parts and one equal part being considered is the “real-thing fraction.”
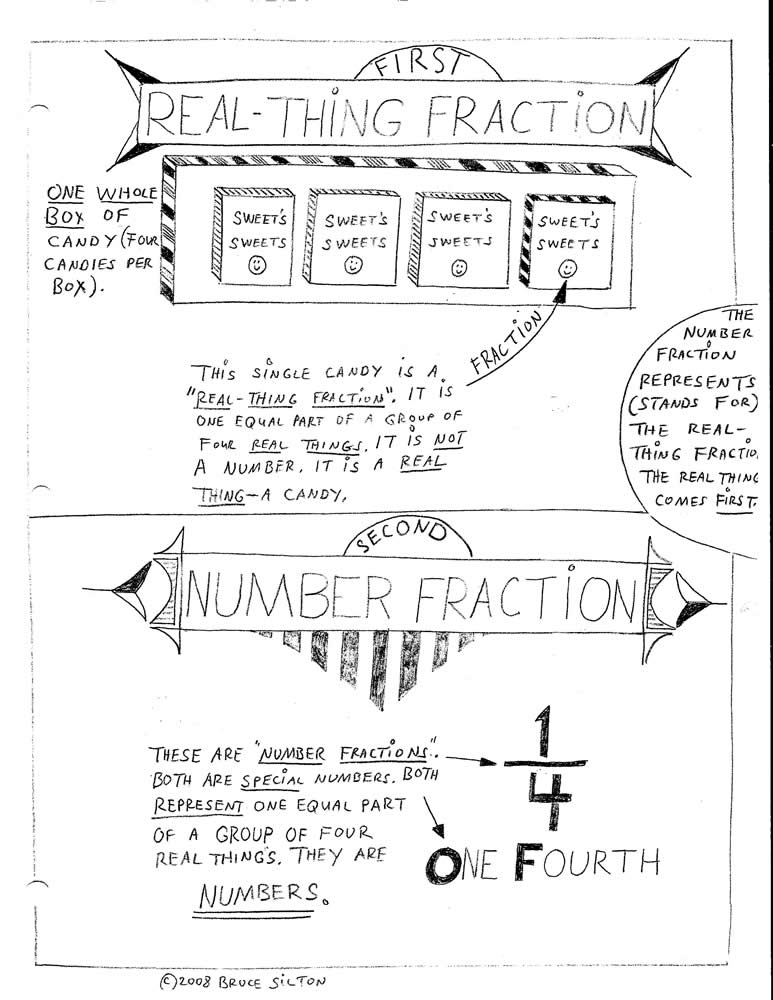 The Real-Thing Fraction (2008)
The Real-Thing Fraction (2008)
Sometime later, I corrected my mistake.
Then, in 2014, I gave the “real-thing fraction” a new name: the “fraction-thing.” “Fraction-thing” is shorter, easier to say, write and remember. This discovery is fully written up in my book, The Fraction Solution. Data on the fraction-thing and how to use it also appears in the “Fraction Solution” paper on my math educator’s website: Math Creativity.com.
In Part 14 of The Fraction Solution, I re-defined the fundamental components of the mathematical fraction using the idea of a fraction-thing.
DEFINITION OF “FAMILY”: A group of people or things with essential characteristic in common.
DEFINITION OF “FAMILY OF FRACTIONS”: Each of the three forms of the math fraction (common fraction, decimal fraction and percent) has essential characteristics in common with the other forms of the math fraction. All three are solely and only numbers. Each form is used to represent the equal parts of a thing or a group of things — the fraction-thing. Each carries out this function by means of a numerator and a denominator. Because of these common characteristics, the three forms of a fraction may be considered a “family of fractions.”
DEFINITION OF “FRACTION-THING”: A fraction-thing is defined as the actual physical thing or the group of actual physical things separated into equal parts that the math fraction (the number) represents. The fraction-thing includes all the equal parts of the thing or group of things plus those specific equal parts being talked about or being considered.
DEFINITION OF “FRACTION”: Any number that uses a numerator and a denominator to represent a fraction-thing.
DEFINITION OF “DENOMINATOR”: The denominator is a number that shows the total number of equal parts the fraction-thing has been separated into.
DEFINITION OF “NUMERATOR”: The numerator is a number that shows how many equal parts of the fraction-thing are being considered.
DEFINITION OF A “COMMON FRACTION”: A common fraction is a math fraction (a number) with the denominator written below a line (the fraction line) and the numerator written above the fraction line. Common fraction denominators can be a numeral of any size (1/5, 3/14, 2/35, 24/125, 66/2,048…). A common fraction represents a fraction-thing.
DEFINITION OF A “DECIMAL FRACTION”: A decimal fraction is a math fraction (a number) with the numerator written to the right of a special point – the decimal point, which separates whole numbers (written to the left of the point) from the fractions (written to the right of the point). The denominator of a decimal fraction is the place value of the digit written farthest to the right of the decimal point. Decimal fraction denominators must be 10, 100, 1000…. A decimal fraction represents a fraction-thing.
DEFINITION OF A “PERCENT”: A percent is a math fraction (a number) with the numerator shown by a numeral written to the left of a special sign (%) — the percent sign. The percent sign always represents a denominator of 100. A percent represents a fraction-thing.
This first illustration shows a fraction of a group.

And this second picture shows a fraction of a whole thing.

Still later, I began extrapolating on the idea of a fraction-thing and how it might be useful at higher levels of math.
From those thoughts came this description of a fraction-thing written up in Appendix C of my paper, The Fraction Solution:
A DESCRIPTION & DEFINITION
OF A FRACTION-THING
One definition of “quantity” is anything which has the property of being measurable.
Within its perimeter, our physical universe is composed of a variety of QUANTITIES.
Any quantitative aspect of our physical universe, whether existing at a fixed or changing rate, such as
- any piece or unit of MATTER, however vast or small,
- any amount and kind of ENERGY, whether nuclear, mechanical, etc.,
- any SPACE (length/area/volume, etc.) of any dimension, from the diameter of a subatomic particle to spaces millions of light years in extent,
- and any amount of TIME measured in units from nanoseconds or smaller to life cycles of suns and whole galaxies
can be separated into equal parts (or considered to be separated into equal parts) for the purpose of making observations and calculations about those equal parts and then used as a FRACTION-THING .
These fraction-things can then be represented by common, decimal or percent fractions composed of just numerals or just variables or a combination of numerals, variables, operators and other symbols arranged into meaningful mathematical expressions and equations for the purposes of simplification and/or solution.
The above description and definition of a fraction-thing is a somewhat poetic way of stating the following un-poetic fact: Any part of the physical universe, regardless of bigness or smallness, any piece of matter, any amount or kind of energy or force, any space of any dimension, any amount of time, or any combination of the above components, can be separated (or considered to be separated) into equal parts and then represented by one or more of the three members of the Family of Fractions and calculated upon using the various tools of mathematics.

