The Other Side of Math
∞ PART TWO ∞
THE STUDENT AS A CREATOR
OF MATHEMATICAL KNOWLEDGE
Why do we emphasize freedom in the arts and tolerate an absence of creativity in math? Isn’t it odd that educators can demonstrate trust and respect for a young student’s creativity as a writer of both fiction and non-fiction (as well creativity on the performance stage and in the art studio) while at the same time requiring that same student to work only within the restricted boundaries of an intentionally limited set of mathematical tools from kindergarten through 12th grade?
Some students can flourish within our current math system….

…but many can’t. How do we include those who can’t?

Traditionally, because it is an exact science, creative activity in math has been left to extremely advanced levels of training, as in graduate and post-graduate programs specifically designed to foster new ideas. However, many students who have the intellectual potential and innate purpose to reach such elevated levels of training are, as children, too frequently dissuaded from doing so by the restricted way that math is taught at the elementary and secondary school level.
This problem can be directly observed by noticing the difference between the popularity of the English language versus the language of math. When I walk through the corridors and recreation areas of the school where I work as an academic tutor, I often see boys and girls reading: they read standing up, lying down, sitting cross-legged on the concrete walkway or grass while eating their snacks and lunches, even while walking! These students have cast their ballots and (best estimate) 99% of them voted to read.
Where are their math books?
There are simple methods of encouraging an outflow of mathematical thought and action from the student to others that can be lightly introduced as early as first grade, begun in earnest in the third and continued thereafter until the student graduates from high school. And even after graduation, these same methods can be used continuously throughout a student’s college and graduate school studies. The result? More of our young people will find successful careers and lives using math and the math-related sciences. Personally, I hope that some of these – many or few — in their role as scientists and mathematicians, will contribute mightily to mankind’s fund of useful knowledge.
 TOWARDS A COMPLETE MATH EDUCATION
TOWARDS A COMPLETE MATH EDUCATION
In order to improve the overall quality of the math education we deliver to our students, most educators know the vital importance of students grasping conceptually the meanings of the key terms of basic math, learning the math facts cold and becoming skilled users of the essential mathematical theories, axioms, theorems, and algorithms. However, even gaining mastery over all of the above – a major challenge in itself — will not enable our students to realize their true potential for success with mathematics over the course of their lives. Even when they are uniformly doing well on their math courses, when they are progressing through them on target, there will still remain vital elements of a complete math education that are missing from current math curriculums.
The situation can be simply stated:
In most schools, the student is required to accept one set of mathematical theories, axioms, theorems, definitions, procedures, problems, solutions, and rules without the opportunity to either learn about others or create his own.

By fixing the students’ attention and interest upon one particular mathematical system, such as that represented by a school’s current series of math texts, workbooks, glossaries and examinations, they are to that degree placed at effect of the subject rather than at cause over the subject.
 THE MATHEMATICAL BOX:
THE MATHEMATICAL BOX:
THE UNIVERSE OF THE STUDENT

VERSUS
THE UNIVERSE OF THE BOOK

Viewed from an exterior viewpoint, the situation would look like this: During the thirteen most formative years of a young person’s life, the student is placed inside a single mathematical system and required to remain there. Using an expression common in 21st Century America, the student is located inside a box, but he is not informed that he is in a box — or even told that the box exists.
It is not that the box itself is necessarily bad. It isn’t. In my work as an academic tutor, I use both a Macmillan and a Saxon series of math texts. Both are terrific teaching and learning tools. But good or bad, each textbook series represents only one mathematical viewpoint, one set of useful truths and tools. In the student’s eyes and mind, however, the book’s theory, algorithms, problems and solutions become now and forever THE theory, algorithms, problems and solutions. Pass the test. End of story.

This is not a healthy educational state of affairs for a sane, inquiring mind.
There are other paths the student never learns about. Literally never. The most important of these missing paths is his own…

… and that is the one we actually must foster if we intend to produce an abundance of creative mathematicians, physicists, engineers and other professionals whose work depends on math.
Our practice of presenting only one consistent viewpoint – however excellent that viewpoint may be – leaves no room for a students’ inborn creativity. After being handled in this way for a number of years, few of them will “escape the box”.
Yet they must systematically venture outside the limits of their school’s official math system if we want them to discover a creative life in math or the mathematically-based sciences, such as physics and chemistry.
In most cases, an individual’s purpose in learning, using, and creating with math must be intentionally, systematically and continuously aroused and maintained by a program designed to do precisely that and which is staffed by faculty who intend to produce powerful math kids and adults as well as mathematicians and scientists capable of contributing exceptionally valuable products, services and knowledge to mankind.
 MAKING POWERFUL MATH KIDS
MAKING POWERFUL MATH KIDS

Although some curriculum developers, teachers, tutors and other educators try hard not to aim their students in the direction of only inflowing knowledge, the overall tendency is towards accepting the other-created knowledge extant in math textbooks, workbooks, glossaries and examinations.
From the school’s viewpoint, the student is a student, not the teacher.
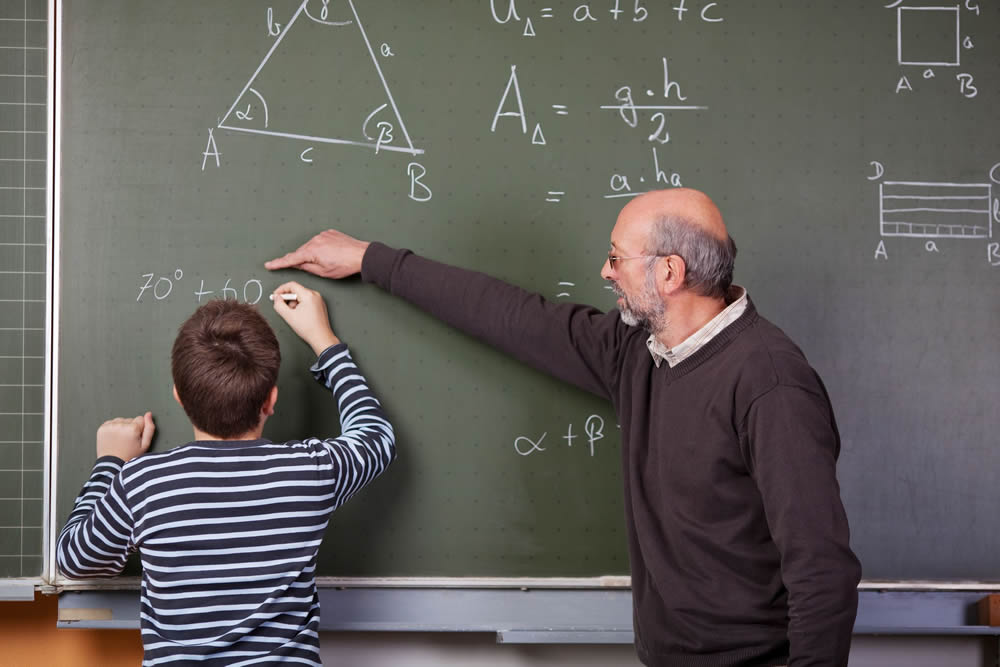
Everyone knows that the student did not write the math book he is studying, that he did not formulate the test questions used to evaluate his progress.
If the student’s teacher is competent both mathematically

and as a teacher,

if his textbook is a good textbook, and if the tests and its grades are fair, the student will receive the accumulated mathematical knowledge and wisdom considered necessary by the curriculum authorities in his school system to educate a human being for the particular subject being taught, whether it be Arithmetic, Pre-Algebra, Algebra 1, Geometry, Algebra 2, Trigonometry, Pre-Calculus or Calculus.
But let’s take the student’s viewpoint: the teacher, book and exams represent an impressive and apparently omniscient (all-knowing) creativeness which is (at best) hard or (usually) impossible for the student to disagree with, argue against, add or contribute to.

Thus, the student faces a continuous inflow of math knowledge for some 13 years.

What if we, as teachers, want to assist the student to develop his own powerful, mathematical mind? How do we assist the student to find his way out of and beyond the apparently overwhelming creative power presented to him by his school, book, teacher, and exams? How do we build or re-build the students own innate mathematical power?
It is definitely not true that the student’s universe and the universe of his book are opposed to one another. The student can and, in most cases, should leave the box (school, teacher, book and exams) without either rebelling against them or abandoning them. He can be coaxed and gently guided out-out-out on an oh-so-gradual basis, taking with him all that is genuinely useful to him.
When this process is done correctly, it will be found that he has, by his own decision and according to his own good judgment:
(1) Retained a great deal of the textbook’s knowledge and skills exactly as taught,
(2) Altered or added to other lessons, and
(3) Wholly discarded still other aspects of the book’s teachings, replacing these discarded elements with ideas, methods, knowledge and skills he has determined are valuable to his life.


