The Other Side of Math
∞ PART THREE-A ∞
FUNDAMENTALS
ON THE OTHER SIDE OF MATH

The Other Side of Math
 OSOM IS AWESOME
OSOM IS AWESOME

The “Other Side of Math” is abbreviated to “OSOM.” And “OSOM” is pronounced like the word “AWESOME”.
 PROBLEM CREATION, PROBLEM SOLVING,
PROBLEM CREATION, PROBLEM SOLVING,
AND ANSWER CHECKING
DEFINITION OF PROBLEM: A STATEMENT REQUIRING AN ARITHMETIC, ALGEBRAIC, GEOMETRIC OR OTHER MATHEMATICAL SOLUTION (ENCARTA WEBSTER’S DICTIONARY).
DEFINITION OF CREATION: THE ACTIVITY OF BRINGING IDEAS, THINGS, OR EVENTS INTO EXISTENCE. ALSO, THE IDEAS, THINGS OR EVENTS THEMSELVES THAT HAVE BEEN BROUGHT INTO EXISTENCE.
OBSERVATION: My students uniformly experience improved understanding and performance in mathematics when I have them create their own math problems, solve their problems and then check their own answers.
“Problem Creation” is done as an educational activity in addition to — not as a substitute for — solving their textbook’s problems after they have mastered their book’s exercises.
 I AM IN GOOD COMPANY…
I AM IN GOOD COMPANY…
DEFINITION OF “ORIGINATE”: TO INVENT SOMETHING, OR BRING SOMETHING INTO BEING.
IT IS AN EDUCATIONAL TRUTH THAT STUDENTS LEARN MORE WHEN THEY ARE PERSONALLY INVOLVED IN THE STUDY OF A SUBJECT.
AND THEY LEARN EVEN MORE WHEN THEY APPLY WHAT THEY HAVE LEARNED TO LIFE OUTSIDE THE CLASSROOM.
Few teachers rely solely on their textbook. Most heighten student involvement by getting their students to create something on their own quite in addition to mastering the textbook materials. The list of such creative activities is long – and grows longer as teachers everywhere apply their ingenuity to solve this problem. Some creative techniques are so well known and so universally effective that they are often built right into curriculums as requirements:
- For Science Fair projects: Physics, chemistry, and biology students learn the scientific method by carrying out scientific experiments derived from their own observations of the natural world. They test their hypotheses in the world outside the classroom and then announce their findings to the school using presentation boards.
- Students produce their own magazines and fill the pages with non-fiction articles, poems, short stories, and art originated by the students themselves.
- After reading the books on their required reading lists, they write essays based on their personal viewpoint of the book.
- In creative writing classes, they invent plots, describe their made-up characters in detail, and, from whole cloth, devise tragic lives or happy endings.
- How do you bring history to life? Students of history write essays that demonstrate a personal understanding and interpretation of historical topics. And after carrying out research, they give talks to the rest of the class about the people, periods, and events being studied. (More unusually, history teachers have been known to literally bring history to life by mobilizing an entire class to write scripts, produce and portray on stage the people and events described in their textbooks.)
- In government and civics classes, students originate, participate in or contribute to student government. Essays are often required, as well as talks where they communicate their own ideas for improving one or more aspects of local, state or national government.
In this way, teachers invite, coax, require, and even demand that their students CREATE to achieve higher rates of real learning. Many teachers, tutors, curriculum developers, and school administrators are committed to this approach. Whether they are asking their first graders to stop copying the book’s noun-verb-noun sentences and start writing their own noun-verb-noun sentences or enlisting older students to design and paint scenery for school plays or assigning the team’s best football players or cheerleaders to mentor the team’s newest members, they are using a creative process to enhance learning.
I also use a variety of creative exercises and activities in every subject that I teach This includes having them apply what they have learned to actual people, things, and situations beyond their textbook and classroom.
In addition, when I am teaching mathematics, I systematically apply Problem Creation after each major and minor math topic is mastered, as described in detail in this book on “The Other Side of Math.”
BECAUSE THAT IS WHAT IT TAKES TO START THE PROCESS OF FREEING STUDENTS FROM THE MATHEMATICAL BOX.
In 2007, the uniform workability of Problem Creation was in the provisional stage — it seemed possible that it might work broadly when used with all my students. Today, in 2017, after ten more years of one-on-one testing, refining and continued application of this idea during additional thousands of tutoring sessions, it has gained in my mind the status of “workable truth” because I have seen Problem Creation work time after time after time.

A Student Invents His Own Math Problem
In this way, they do not rely on their textbook as the sole source of learning exercises. This fostering of the independent creation of mathematical problems, problem solving, and answer checking by the individual student raises that individual from a condition of relative, passive effect to a condition of greater, active cause and creativity in his understanding of math and increases his ability to use math successfully in his life.
 FIRST PRINCIPLE
FIRST PRINCIPLE
Definition of Principle: A basic assumption; an important underlying law or assumption required in a system of thought. (Encarta Webster’s Dictionary of the English Language, Second Edition)
The following assumption underlies every aspect of this book. This assumption is a fundamental principle in my personal philosophy of education.
There is an innate requirement within each individual to act in a creative manner. This innate, creative power is strongest when directed towards achieving goals set by the individual himself.

When this inborn drive is thwarted in any way by a particular subject (for example, mathematics), then, to that degree, the individual’s genuine interest, productivity, value and general happiness in learning and using a subject (for example, mathematics) is reduced away from his innate potentials and can eventually reduce to zero.
The above principle is based upon my observations and experiences while tutoring young people in academic subjects over the last 17 years. Further, it agrees with 49 years of experience as an artist. And it agrees when examined against my experience teaching art to young people.
However, the data in this paper is not intended to prove or defend this assumption. The workability of Problem Creation, Problem Solving and Checking Answers does not depend on either the truth or falsity of my assumption. After successfully applying Problem Creation to hundreds of math students over an eleven-year period (2007-2017), its consistent effectiveness is a fact. Being a practical fellow who is required to take kids in math trouble and return them to their classes with their troubles vanquished, I consider this fact to be senior to any principle, hypothesis or theory.
Problem Creation works.
 EARTH, 2017
EARTH, 2017
CURRENT MATH CURRICULUM

Solving the Math Book’s Problems
Let’s get practical. The steps required to successfully complete (pass) most math courses currently looks like this:
- HERE ARE THE BOOK’S PRINCIPLES, AXIOMS, THEORIES, TERMS, DEFINITIONS, PROPERTIES, ALGORITHMS, RULES, ETC.
- HERE ARE THE BOOK’S PROBLEMS.
- HERE ARE THE BOOK’S SOLUTIONS (THE STEPS USED TO SOLVE THE BOOK’S PROBLEMS).
- HERE ARE THE BOOK’S ANSWERS.
- HERE IS THE BOOK’S EXAM.
- THE END (HE GRADUATES TO THE NEXT GRADE OR COMPLETES HIS SCHOOLING.)
It is my conviction that the above 6 steps are not the best way to educate our students in math.
Yes, it is true that they must be able to execute steps 1-5 with professional competence. But beyond the point of learning currently acceptable math, we could open up any point in the above series and expand it.
Further, we can guide our young people to figure out their own ways to expand any point in it. Especially point #6. This series of steps should NOT end where it usually ends. It should end where the student decides it should end. That’s when something wonderful could happen.
But for that to happen, each of steps 1 to 6 must be altered to promote an outflow of knowledge: knowledge that originates within the student and which is then communicated outward to others.
If this transformation is conducted skillfully, some of these boys and girls may one day be able to create each of the above steps on their own creative initiative using their unique personal viewpoint of mathematical theories, axioms, theorems, definitions, algorithms, problems, solutions, exam and — what’s next? But to reach such a viewpoint, we must free our students from the box they have studied within and been required to accept. And freeing them up starts right now in the first, second, third, fourth, fifth grade and beyond.
 EMPOWERING
EMPOWERING
THE UNIVERSE OF THE STUDENT

DEFINITION OF “EMPOWER”: (1) TO GIVE SOMEBODY POWER OR AUTHORITY; (2) TO GIVE SOMEBODY A GREATER SENSE OF CONFIDENCE OR SELF-ESTEEM. (ENCARTA WEBSTER’S DICTIONARY OF THE ENGLISH LANGUAGE)
The Other Side of Math consists of a series of study actions that, when properly applied, empower the student to bring into existence his own ideas and uses for mathematics.
In OSOM, at an early age, the student is asked to begin the process of originating math problems, definitions, procedures and ideas on his own. All students are considered to be capable of doing this. This process is begun by asking him to perform small, easily accomplished tasks that require him to think and do mathematically on his own without the direct assistance of either his book or his teacher.
THE VERY FIRST AND SIMPLEST OF THESE OSOM TASKS IS TRAINING INDIVIDUAL STUDENTS TO CREATE MATH PROBLEMS WITHOUT THE HELP OF TEACHERS OR MATH BOOKS, SOLVE THOSE PROBLEMS AND THEN CHECK THE ANSWERS.
For most students, these study steps will only lead to an increase in ability to use math successfully in their lives — lives in which math plays a necessary but subordinate role.
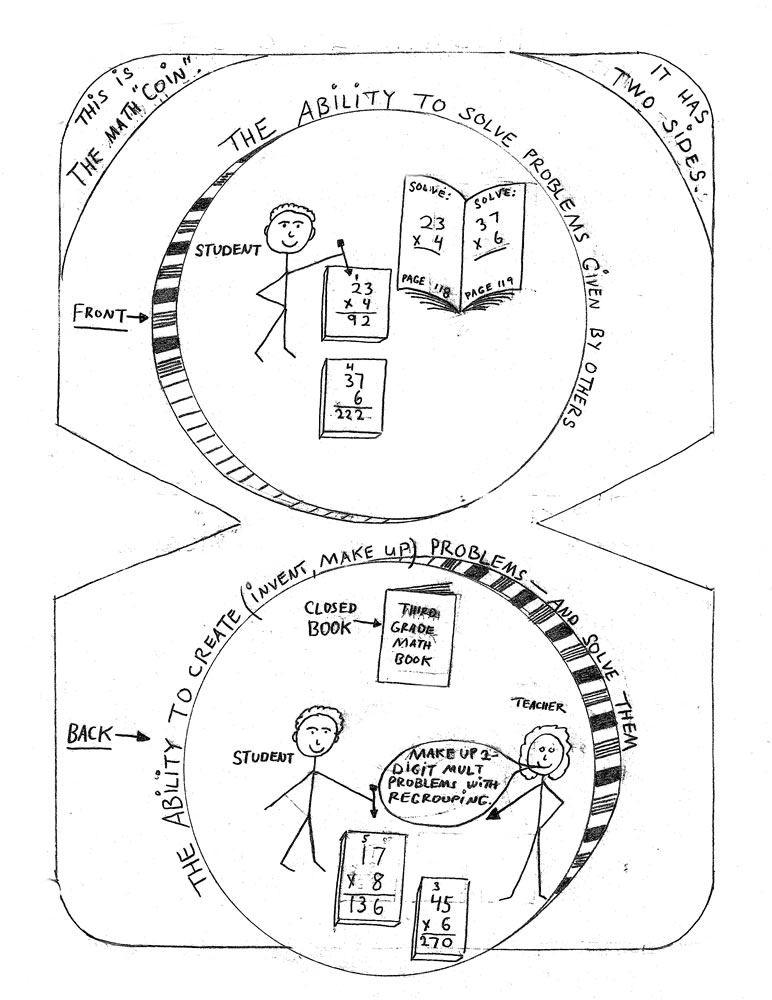
The Two-Sided Math Coin
Others, I hope, will use OSOM to achieve life goals in which math is applied at an advanced, professional level as in computer science, applied and theoretical physics, medicine, economics, electronics, engineering, accounting, insurance, industrial chemistry, architecture, music composition, aerodynamics, etc.

For perhaps only a few, OSOM will lead to the discovery of natural laws that will change our planet dramatically.

Sir Isaac Newton (1642-1727) discovered the force of gravitation, invented the mathematics used to reach the Moon and Mars (calculus), formulated the three natural laws governing motion… and much more.
As an example, one of my dreams and intentions is that OSOM students, mathematicians and scientists will discover, develop and bring to market cheap, plentiful, 100% non-polluting energy sources that can be made available to EVERYONE so that energy is no longer a relatively scarce commodity that can be employed to manipulate people and bring about anti-social situations like war and economic hardship.

First Prize Goes to Hobie Smythes!
 THE SIX STEPS OF OSOM
THE SIX STEPS OF OSOM
 The Math Demon, 2009
The Math Demon, 2009
OSOM is comprised of six separate, major steps, starting with study actions which can be implemented into current curriculums and ascending to those steps requiring the development of new courses with their related materials.
Step 1: PREREQUISITE: MASTERY OF CURRENT MATH TOPIC
Step 2: PROBLEM CREATION, PROBLEM SOLVING AND CHECKING ANSWERS
Step 3: STEPPING OUT OF THE BOX WITH ALTERNATIVES:
Alternative Algorithms, Alternative Axioms, Alternative Theorems, Alternative Numeration Systems, Alternative Solutions, Alternative Methods of Checking Answers, Alternative Definitions
Step 4: INSPIRING EXAMPLES FOR KIDS TO LEARN FROM:
The History of Mathematics — Mankind’s Math and Science Greats
Step 5: IDENTIFYING THE TARGET:
Mankind’s Past, Current, and Future Technologies –
the Good, the Bad and the Ugly
Step 6: EXTRAPOLATION, DISCOVERY AND INVENTION:
Good Ideas, Better Ideas, Big Ideas
This book on The Other Side of Math” presents and develops in detail only OSOM Step 1, Prerequisites: Mastery of Current Math Topic, and OSOM Step 2, Problem Creation, Problem Solving and Checking Answers.
The Appendices of this book contain previews of OSOM Steps 3, 4, 5 and 6.
………………………………..
Note: The complete name of OSOM Step 2 is: “Step 2, Problem Creation, Problem Solving and Checking Answers.” This is a long name to keep repeating! So, in the remainder of this paper, it will usually be shortened to simply “Problem Creation” or sometimes, “Step 2.” Thus, when you read “Problem Creation” or “Step 2” that usually indicates all three mathematical actions: “Problem Creation, Problem Solution, and Checking Answers.”
 MY EXPERIENCE AS A MATH TUTOR
MY EXPERIENCE AS A MATH TUTOR

This brings up a point that should be of interest to readers of this book: my overall experience in educating children both in math and other academic subjects.
I am 74 years old and have worked as a tutor on the faculty of a private school since March of 2000. In this 17 year period, I have given 17,000+ tutoring sessions. Approximately 10,000 of these tutoring sessions have been devoted to helping students with their mathematics.
As a math tutor, my day-to-day work consists of helping individual students who, while studying in their classroom, are not progressing well in their academic subjects, including, of course, mathematics.
I work in a quiet office with one student at a time. Using a wide range of study methods, tools and skills, I help that student gain full understanding of his material so that he can now make adequate progress in his reading, writing, math, etc.
When the student’s difficulties appear to be fully handled, I return him to his classroom. He resumes work with his class. My work is completed when, by actual follow-up in the classroom, both the teacher and I can see that the student is now progressing successfully in his reading, writing, history, science, math, etc.
If he is still not learning easily and happily in that subject, he comes back to me. I then continue the tutoring until he is a happy, progressing student.
Most of my students are in kindergarten through fourth grade. I also work with older students, from fifth grade through twelfth grades, as needed by the school.
(At the end of this book you can find a selection of the successes my math students and their parents have had, written in their own words.)
 APPLYING PROBLEM CREATION IN TUTORING
APPLYING PROBLEM CREATION IN TUTORING

Infinity is a Very Large Number (2014)
In my mind, the effectiveness of Problem Creation is a fact. Well, what does this fact consist of?
As described above, when I work with young people, my purpose is to produce a happy, able student who is again progressing in his math studies, who enjoys learning math and who can again work successfully in the classroom. Inevitably, as part of this one-on-one teaching process, the moment arrives when it appears I have handled the student’s confusions. He appears to now understand his math. He can now accurately perform calculations on the same textbook problems he could not handle before the tutoring. He seems to understand everything we have covered in his tutoring sessions.
But before I end off and send the student back to his regular class to continue his studies, I want to know if he truly understands the materials he was stuck on or has he merely gained a somewhat limited, mechanical ability to solve the books’ problems that might relapse when he is separated from my one-on-one help.
Can he, with the book firmly closed, create, solve and check his own problems and demonstrate true understanding of every principle and every step involved in the solution up to his current level of schooling? If not, then he does not understand that math. The tutoring must continue until he finally does understand the principles and algorithms of that math and can easily create his own problems, solve and check them.
Thus, by direct testing, trial and error and after years of repeated observation of elementary, middle and high school students in and out of the classroom, I have determined that those of my students who successfully complete the Problem Creation process with me in my tutoring sessions on a single, specific math topic have now attained a higher level of certainty, understanding and ability to use that one topic than I could have achieved without using the Problem Creation process.
 THE TWO PREREQUISITES
THE TWO PREREQUISITES
Problem Creation only works when the following two conditions have been met:
FIRST CONDITION
The student has already mastered his current math topic. For Problem Creation to be successful each and every time it is used, this first condition must be accomplished: mastery of current math topic.
SECOND CONDITION
Problem Creation is delivered by a teacher or tutor who has the intention to enhance the student’s abilities and whose classroom or office is a safe learning environment.
Problem Creation is unlikely to produce the expected, excellent outcome in a hostile, threatening or chaotic environment. When used in conjunction with bad manners, an authoritarian teacher, a hostile attitude, or an unsafe learning environment, Problem Creation not only does not work but the student gets worse. (I know, because I have done Problem Creation the right way and the wrong way!)

