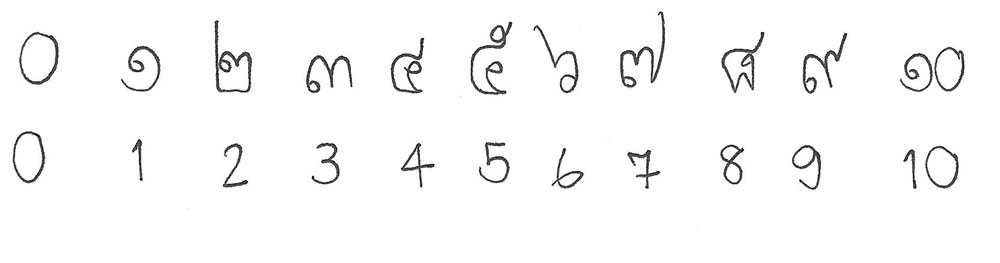The Other Side of Math
∞ PART FOUR ∞
THE TRUE HISTORY OF MATHEMATICS
FOR THIRD GRADERS
 THE TRUE HISTORY OF MATH
THE TRUE HISTORY OF MATH
FOR THIRD GRADERS
(Inside a tutoring office in an elementary school somewhere on Florida’s West Coast)
Tutor: “Hobie, you’ve gotten really good at solving these 4-digit subtraction problems. You understand place values through thousands. You can regroup across three zeros without making mistakes. You can use addition to check the differences, just like the book says. What a good job! Gimme five, big guy!”
(The small room echoes with the sound of two hands smashing together in midair.)
“Now, please close your math book. This morning is special because you’re going to start being your own math teacher and writing your own math book.”
Student: “Wow, Bruce, you’re scary! Did I do something wrong? And what’s wrong with our math book? I like my book.”
Tutor: “You? Wrong? You’ve done nothing wrong. Zero! And you didn’t make any math mistakes either. Fact is your math is close to perfect. Talk about scary! That’s why you get to be your own teacher for awhile; you earned this. And though our math book is a really good one, did you know it’s not the only math book for third graders?”
Student: “Hold on now! Really? Come on! There are other math books?”
Tutor: “Sure. Other third grades in other schools use different books. And other countries in different parts of the world use their own books. Some look a lot different than this one. Plus some of those other books teach different ways of doing math. And some teach different ideas about math. Goofy as it sounds, some books have different numbers in them, too?”
Student: “How could they be different? Isn’t a 3 just a 3?”
Tutor: “Well, yes, of course the idea of three is still three. It’s just that they write all their digits and numerals differently, so their digit 3’s don’t look like our digit 3’s.”
Student: “Bruce, that hard to believe! You better prove it; let’s see one of these other 3’s.”
Tutor: “OK, Hobie, here goes. I’ll make two: a fat one and a skinny one.
(The tutor draws two digit 3’s based on the classical digits of Thailand.)

I think I like the skinny one better.”
Student: “Nice! But I like the fat one. Let me make one. Hey, mine is nice, too! So that’s a 3? Are you sure it’s not just a bunch of pretty squiggles?
Tutor: “Yep, but only in Thailand, not in Florida. Obviously you know the way we subtract, but did you know that many people in other places don’t subtract the same way we do?”
Student: “Gee, Bruce, are you making jokes again?”
Tutor: “Look, I’m not making this up. Let’s make a deal: If you do a really good job being your own teacher and writing your own math book, we might have time to learn Thai fives, sixes and sevens. They are really beautiful, aren’t they. Ok, I’m not promising, but if we have time, yes.”
Student: “Cool! And there really is another way of subtracting?”
Tutor: “Absolutely, Hobie. There’s a lot to learn in math. Why, the math that people used hundreds and thousands of years ago isn’t the same as our math. Believe it or not, there was a time long ago when no one had the digit zero. So how do you do math without the zero? Tough, huh? You see, math changes, grows, and improves. You can be really sure that a few hundred years from now math will be different than today. That’s because smart math kids like you will grow up to be smart mathematicians who can figure out new and better ways to find out how many and how much. There are probably lots of things that can be done with numbers and shapes and sizes that we haven’t even dreamed of yet.”
Student: “Wow! Way Cool! No zero? Yikes! But, Bruce, how else can you subtract? Gosh, I’d like to learn another way to do subtraction. Can you please show me right now?”
Tutor: “Not until you get to 4th grade. First you have to finish 3rd grade math. You have to learn our book’s way of subtracting so well that you just know it no matter where you are or how hard the problem is. If you learn our way of subtracting first, we’ll have fun next year learning a different way. Maybe even two other ways. The coolest other way is how they subtract in Austria.”
Student: “Sort of like learning to print well before learning cursive?”
Tutor: “Yes, exactly; we learn in steps, taking one step at a time.”
Student: “OK, I’ll wait. But, Bruce, can you at least tell me how come we do subtraction our way?”
Tutor: “Good question. The short answer is we picked it because it’s a fast, accurate way of finding out how many are left. It works and most kids learn it easily.”
Student: “OK, but now why do I have to make my own problems? This book has got tons of them. Look at all these problems — page after page of problems. I’ve already solved them all.”
Tutor: “Well, sure your books are filled with problems. But there’ll be lots of times in your life when you won’t be in school, when you’re working or at home or at play or in sports or in a store and you’ll need to subtract, but the math book won’t be there and I won’t be there . In fact, when you’ve finished school and find yourself living and working as an adult, there simply won’t be math books or teachers giving you the math problems you have to solve. Police, doctors, soldiers, pilots, business people, mothers with kids, dads, baseball players, EVERYONE is faced with lots of math problems – including subtracting across zero problems that can only be solved if, without a book, they can use the kind of math you have just learned. AND you will not only have to make up the problem, you have to figure out the right answers and check the answers!”
Student: “If that’s so, I think I’ll be a kid for a long time.”
Tutor: “Ha! We’ll see about that. OK, ready for some fun? “
Student: “OK, I give up!”
Tutor: “Smart decision! Please close your book. Let’s see you be your own teacher and create some math. We’ll start by having you make up a 4-digit subtraction problem. Use your own numbers, not the numbers of the book’s problems. Remember, different numbers. Your first problem should have zeros in the hundreds’ and tens’ and ones’ places. Make the problem so that you must regroup from the tens’, hundreds’ and thousands’ places. Same as your book’s problems.
Student: “Easy peezy lemon squeezie. There!”
Tutor: “Yeah, exactly right. Now find the difference.”
Student: “OK, done.”
Tutor: “Right on as usual. Check your answer.”
Student: “Yups, I done did it.”

Tutor: “Good job. Ready for the next question? Why did you borrow from the thousands place? Demonstrate your answer by using these ones, tens, hundreds and thousands place-value manipulatives to show your numbers — especially the borrowing.”
Student: “Hey, this is hard! I’m lost. Can you please help me?”
Tutor: “No, Hobie, you can do it. You did it before when the book was open. You don’t need me. Do monkeys need another tail? Do elephants need two trunks? That’s right… Just like that…There! You did it! See, you didn’t need me or the book.
“OK, here’s the next one: Why did you check your subtraction answer by adding? Using these same pieces, can you show why that works””
Student: “You mean like this?”
Tutor: “Perfect. Do you remember telling me how much you want to be an actor? Well, when would an actor need to use 4-digit subtraction across one, two or even three zeros?”
Student: “Probably when he buys things, ‘cause you have to subtract when you buy things.”
Tutor: “Right on. Now create a similar 4-digit subtraction problem like the kind you as an actor would need to solve.”
Student: “OK. Let’s see…“
Tutor: “Take your time.”
Student: “Don’t worry, Bruce, I won’t blow it…There!”

Tutor: “Wowza, good math, Hobie! Ah, that’s a good one! That’s a real problem because, like you say, good actors can make a lot of money and then, of course, they have to spend some of their pay for gas and food and, of course, if you’re going to Paris and London and Tokyo, plane rides cost money, so you’ll need to do a lot of subtraction and….
Later…
Tutor: “Hobie Smythe, you’re a good creator of math problems. Good work. Then we’re all done for today. Prize time. No, you can’t have two prizes. One prize for really good math. Would you like one of these dinosaur gliders? Or maybe a purple ninja? A mini-skate board?”
Student: “Wait, wait! I’m still really curious about Austrian Subtraction… and what about writing Thai 5’s, 6’2 and 7’s? Do we have time to…”
Much later…