THE FUTURE OF NUMBERS
by Bruce Silton
AUTHOR’S NOTE
The word “House” in the title of this paper is a metaphor representing the vast range of products, services and influences derived directly or indirectly from the use of imaginary and complex numbers in modern technologies. The effect of these numbers on the daily life of ordinary people in the twenty-first century is profound — but invisible to the uninformed observer.
My purpose and hope for this paper is simple — to bring greater understanding and appreciation for the mathematical universes that exists somewhere off the number line.
Bruce Silton
Pinewood Village
December, 2016
ACKNOWLEDGMENTS
Any artist who is daft enough to venture into the universe of imaginary and complex numbers at the age of 73 needs an equally daft cheerleader (of nearly equal age) to cheer the result. Thank you, Leslie Silton, for your enthusiastic cheers. You brightened my day when the light was dim!
A good math book is more valuable than a treasure chest filled with silver, gold, platinum and precious gems. My deepest thanks to John Harold Saxon Jr., West Point graduate, decorated officer, test pilot, engineer, math teacher, author and publisher of the Saxon math textbook series, for giving me a fine Algebra 2 textbook (Algebra 2, Second Edition, 1997 by Saxon Publishers, Inc. Norman, Oklahoma.)
DEFINITION OF “IMAGINARY”
You can say that something is imaginary if it exists only in the mind, but does not exist in the real world.
The Future of Numbers
∞ PART ONE ∞
INTRODUCTION:
THE THEORY OF MATH HOLES
I admit it; I like mathematics. My idea of an enjoyable evening is using my native smarts to figure out new ways to check answers to algebra, geometry or trig problems.
It gets even worse (or better)! Each morning I look forward to learning the new math concepts and skills presented in the next lesson of my current math textbook.
And when I see the “100%” handwritten at the top of my exams? Wow! That’s happiness and pride of accomplishment.
Professionally, I have a powerful purpose to help kids, so I take deep pleasure in using the math ideas and tools I have learned to successfully tutor children and young people having trouble with their own math courses.
And now I’ll tell you a secret: I even enjoy the occasional trouble I get into while trying to comprehend and use a totally new math concept!
So you won’t think I’m nuts, I’ll let you in on my “Theory of Math Holes.” It’s simple: a “Math Hole” is what you fall into when you don’t understand the math you’re supposed to be learning or applying.
And my theory? The deeper the hole you drop into, the greater the happiness when you finally climb out.
Naturally, Math Holes come in varying depths. Shallow holes? Phfft! A dime a dozen. I’m in and out of them in minutes, hours or, at most, a day or two. Per my theory, conquering even shallow holes should earn me a few moments of additional happiness. And they do!
But the biggest gains in happiness come from climbing out of the really deep holes – THE MATH PITS.
“Oh, no! A math pit!” I cry, as I freefall into a massive crack in the surface of my mind. “Where is bottom?” I wonder, even as I claw at the sides to lessen the inevitable damage when I strike bottom.
Am I joking? Perhaps a little — but only a very little. Because not long ago, my math universe turned upside down when I stumbled headfirst over the edge of a very deep math hole called “Imaginary Numbers.” Yes, I still managed to get 100% on my exams, but deep inside me, in the innermost core of my math lover’s soul, I knew I did not have a clue; I was just robotically moving symbols around the surface of my paper. I had struck bottom and it was time to find my way out.
Here, then, is the true and uncensored tale of what I learned (and re-learned) as I climbed up and out of the dark and scary depths.
The Future of Numbers
∞ PART TWO ∞
THE NUMBER
WITH THE WRONG NAME
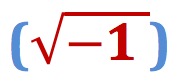
DEFINITION: A “MISNOMER” IS A WRONG OR UNSUITABLE
NAME FOR SOMETHING OR SOMEBODY.
Imaginary numbers are usually introduced to the math student in Algebra 2, the second year of high school Algebra. The very first thing the Algebra 2 student needs to know about “imaginary” numbers is that imaginary numbers are not imaginary.
The word “imaginary” is a serious misnomer when applied to these special numbers because it can mislead students.
Some 400 years ago, mathematicians who did not understand the “strange numbers” that were appearing in the solutions to some of their equations, gave these numbers the wrong name. Today, in 2016, we might (or might not) be stuck with this misnomer, but we are not stuck with false ideas that can rather easily get attached to something that is called “imaginary” but which actually exists.
And “imaginary numbers” do exist. They exist not only in someone’s mind but also in the real world of bees, people and mountains. They are just different than the everyday numbers we have all used since childhood — and when something (or someone) is too different, it is often misunderstood and invalidated.
Factually, imaginary numbers are useful numbers with numerous, important, real-world applications in physics, engineering, mathematics and other modern scientific fields. (The final section of this paper contains an extensive list and description of current real-world uses.)
So what are imaginary numbers and where do they come from? The best place to start is with a simple definition of the word “number.”
WHAT IS A NUMBER?
DEFINITION: FOR EVERYDAY, PRACTICAL PURPOSES, A NUMBER IS AN AGREEMENT THAT A CERTAIN WRITTEN SYMBOL OR SPOKEN SOUND WILL REPRESENT A SPECIFIC QUANTITY OF SOMETHING. A “NUMBER” SHOWS HOW MANY OR HOW MUCH THERE IS OF SOMETHING.
The principal number is “an idea of how many.”
We have numerous ways to communicate our ideas of how many. The three most common forms of numbers are:
- Spoken words (numbers made of sounds waves, as when you open your mouth — actually do this — and say “THREE” or “TWENTY-SEVEN” or “TWO HUNDRED FIFTY SIX.”)
- Written words (numbers made of letters, like one, three, twenty-seven or two hundred fifty-six.)
- Numerals (numbers made of digits, like 1, 3, 27, 256)
There are many less common numbers, like small stones used as counters or raised fingers to show how many scoops of ice cream you want or lines drawn in the sand recording the quantity of hot dogs you devoured at lunch. But regardless of how primitive or sophisticated, numbers show how many or how much.
“How many” is used with things that are easy to count, like apples or people. “How much” is used with things that aren’t as easy to count, like water or sand or air.
Naturally, there are exceptions to the “easy to count” rule. Like money. Money is easy to count, but we still use “how much” when talking about it. Example: “Jane, how much money do you have?”
The Future of Numbers
∞ PART THREE ∞
THREE PREREQUISITES
TO IMAGINARY NUMBERS
FIRST: REAL NUMBERS:
SECOND: SQUARES:
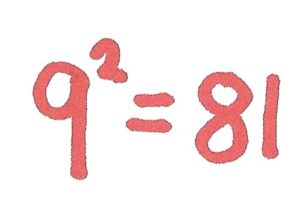
THIRD: SQUARE ROOTS:
The First Prerequisite:
REAL NUMBERS
At this time, there are two distinctly different, major categories of numbers.
> ALL THE REAL NUMBERS ARE IN ONE CATEGORY.
> IMAGINARY NUMBERS ARE IN THE OTHER CATEGORY.
Imaginary numbers are more easily understood when compared to real numbers, so we’ll examine those first.
The “family” of real numbers includes the five different sets of numbers that math students learn about in Algebra One.
a. THE SET OF NATURAL OR COUNTING NUMBERS. These are the same numbers we have been counting with since childhood. Natural numbers do not include 0 because we do not count with 0.
{1, 2, 3, 4, 5,…}
b. THE SET OF WHOLE NUMBERS: Whole numbers include all the natural numbers plus 0.
{0, 1, 2, 3, 4,…}
c. THE SET OF INTEGERS: Integers include all the whole numbers {0, 1, 2, 3, 4,…} plus their opposites, the negatives or opposites of the whole numbers {…,-4,-3,-2,-1).
{…,-4,-3,-2,-1, 0, 1, 2, 3, 4,…}.
d. THE SET OF RATIONAL NUMBERS: A rational number is any number that can be expressed as a fraction with an integer in the numerator and an integer in the denominator. All the following numbers are rational numbers:
> Natural numbers (6, 43, etc.)
> Whole numbers (0, 6, 43, etc.)
> Integers (4 and -4)
> Common fractions (3/4, 6/11)
> Decimal fractions whose digits terminate (0.3, 0.32, 0.325)
> Non-terminating decimal fractions whose digits repeat in a pattern (0.235235235)
> Percents (25%)
Each of these numbers are rational numbers because they can all be written as a common fraction with an integer in the numerator and an integer in the denominator.
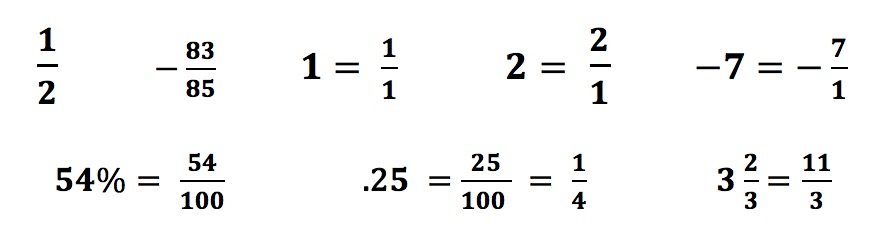
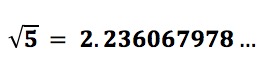
The three dots after the digit “8” indicate that the decimal digits of an irrational number just continue on without end. Therefore, let’s say that an irrational number is a number whose decimal representation is a non-repeating decimal number of infinite length.
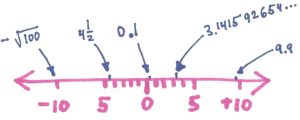
But even though irrational numbers cannot be described by a finite number of decimal digits, and cannot be expressed as an exact fraction of integers, each irrational number still has its own specific location on the number line. Because we can locate an irrational number on the number line, it is called a real number.
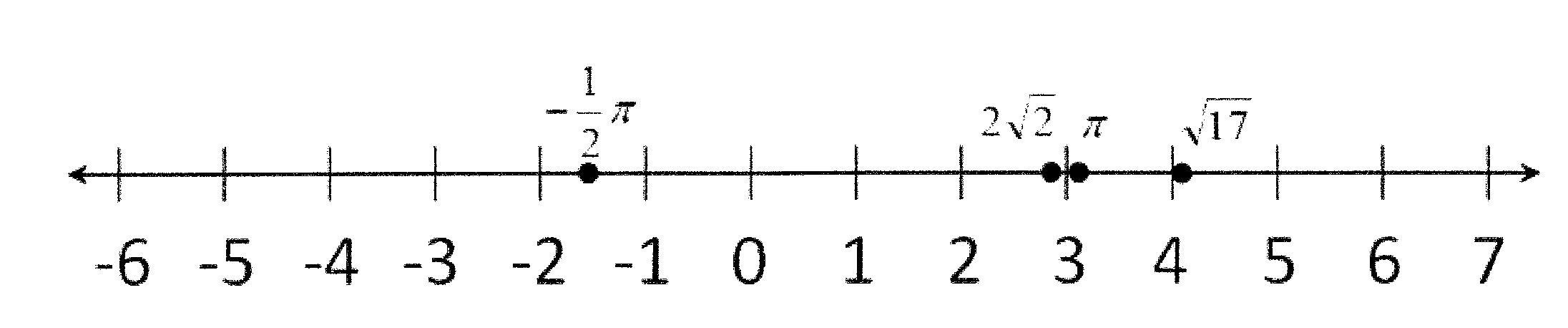
DEFINITION: A REAL NUMBER CAN BE DEFINED AS ANY RATIONAL OR IRRATIONAL NUMBER. THE FOLLOWING NUMBERS ARE ALL REAL NUMBERS.
The above description of irrational numbers includes the relationship between irrational numbers and the number line. This relationship is important. To really understand the idea of a “real number” a student must know what a “property is.
DEFINITION OF PROPERTY: IN SCIENCE AND MATH, A PROPERTY IS A PRECISE POWER OR QUALITY OF SOMETHING THAT MAKES THAT SOMETHING WHAT IT IS.
A few examples of properties will make this clear:
- Soap has the property of cleaning dirt. If the “soap” doesn’t clean dirt off your hands, it isn’t soap.
- Lead has the property of being heavy. If that “lead” isn’t nice and heavy, it isn’t lead.
- Water has the property of freezing at 0 degrees centigrade. If that liquid doesn’t freeze at 0 degrees Centigrade, it is not water.
- Real numbers have many useful properties. Here’s one real-number property:
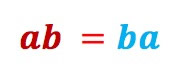
This means that the order of the factors does not change the product. This property is taught to students in 3rd grade when they first learn multiplication.
The set of real numbers has many other interesting and (to a math student, accountant or physicist) extremely useful properties. All five sets of real numbers have in common this property: a real numbers can be graphed on the number line.
Number lines stretch out and out, infinitely far in the positive direction (right) and infinitely far in the negative direction (left) in order to make room for all the real numbers – and mathematicians, as part of their day-to-day math work and being mostly creative people, find, write or think up some very large real numbers, indeed! The number of galaxies in our universe is a really big number. Then when you start adding up all the stars in all the galaxies, those numbers get big!
The number zero (0) is in the middle of the number line. Every real number on this line is a certain measurable distance from zero. That’s an important property of real numbers.
We still need two more concepts—squares and square roots—before defining imaginary numbers.
The Second Prerequisite:
SQUARES
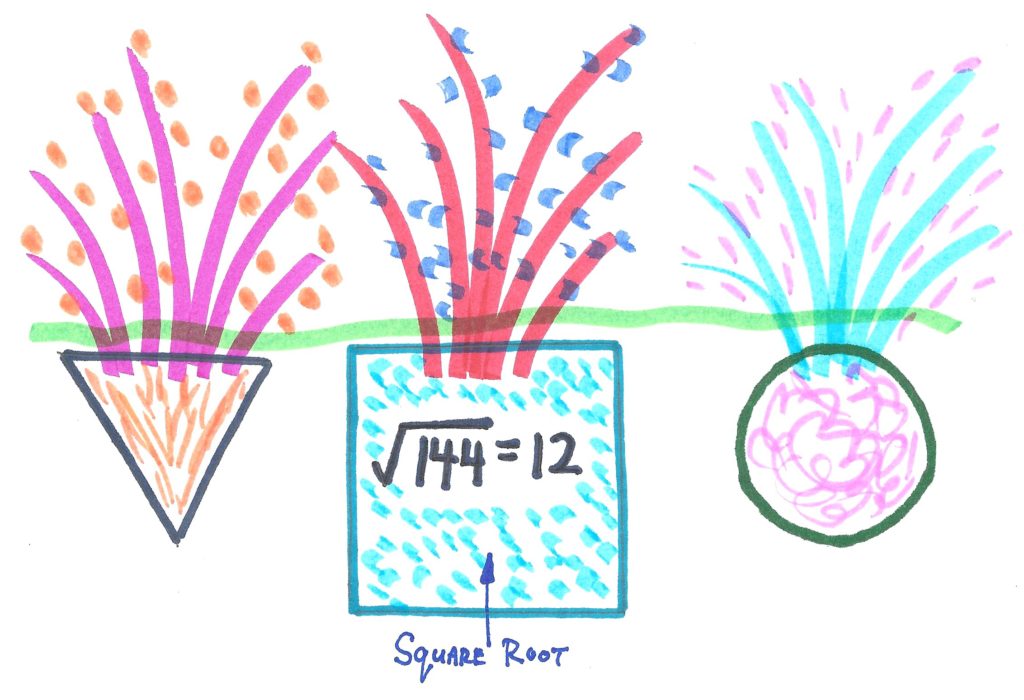
DEFINITION OF “SQUARE” (NOUN): A SQUARE IS THE PRODUCT WHEN A GIVEN NUMBER IS MULTIPLIED BY ITSELF.
DEFINITION OF “SQUARE” (VERB): TO MULTIPLY A NUMBER BY ITSELF.
When you square 5 you get 25.
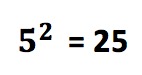
The above is read: Five squared equals twenty-five.
The Third Prerequisite:
SQUARE ROOTS
DEFINITION OF “SQUARE ROOT”: THE SQUARE ROOT OF A NUMBER IS A VALUE THAT, WHEN MULTIPLIED BY ITSELF, GIVES THE NUMBER WE STARTED WITH.
Example: We start with the integer 9. The square root of 9 is a number which when multiplied by itself results in the number 9.
So what number multiplied by itself produces the number 9? There are two numbers that will produce 9.
The number 3 multiplied by itself equals 9:
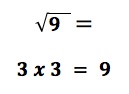
And the number -3 multiplied by itself equals 9:
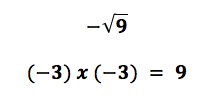Both 3 and -3 will produce 9 when multiplied by themselves.
No, – 9 has no square root. Why? Because any positive or negative real number squared always results in a positive number.
This fact is a property of the multiplication operation:
- Any positive real number multiplied by a positive real number equals a positive real number:
3 x 3 = 9 - Any negative real number multiplied by a negative real number equals a positive real number:
(-3) x (-3) = 9
That leads us to the definition of an imaginary number.
The Future of Numbers
∞ PART FOUR ∞
THE IMAGINARY NUMBER
DEFINED & LOCATED
THE DEFINITION OF AN IMAGINARY NUMBER
All five sets of real numbers can be located on the number line. This is a key datum. All the numbers prior to imaginary numbers could use the number line as their anchor. Just as we use maps to locate ourselves in relation to other locations, we have used the number line to locate the 5 different representations of quantities called real numbers. So, in a very important sense, a person studying mathematics can get “lost” when the numbers no longer correspond to observable, graphable points on a number line.
Once upon a time (but, really, not so long ago), some very smart mathematicians asked themselves an out-of-the-box question (no, they probably didn’t ask this exact question but they did ask a similar one):
“Are real numbers and the number line sacred?”
and gave themselves an equally out-of-the-box answer:
“No.”
Simply put, when you enter the world of imaginary numbers you are stepping off the number line. And when you exit the familiar number line, some (but not all) of the familiar properties of real numbers no longer apply. That fact leads to the primary definition of an imaginary number:
DEFINITION #1: AN IMAGINARY NUMBER IS A NUMBER THAT IS THE SQUARE ROOT OF A NEGATIVE NUMBER.
Here is the square root of a negative number:
That means you can’t look at the number line to find a graphical representation of an imaginary number. Thus, one of the most comfortable and familiar properties of real numbers — that they are measurable as a positive or negative distance from zero on a number line — no longer holds true for imaginary numbers.
GOOD NUMBERS VERSUS BAD NUMBERS?
Definition of “Arbitrary”: An arbitrary idea or action is based solely on personal wishes, feelings, or perceptions, rather than on objective facts, reasons, or principles.
Mathematically, it makes no sense to talk about “good” numbers and “bad” numbers. But it does make sense to talk about “useful” numbers and numbers which are “not useful right now.”
Definition of “Aeronautics”: the science, art, theory, and practice of designing, building, and operating aircraft.
Let’s look at aeronautics in terms of the numbers that are used to solve a typical problem that occurs in that branch of engineering. Each particular aircraft needs the right wings — wings that enable that specific aircraft to fly efficiently and safely and achieve the purpose of that aircraft. Consider this: Imaginary numbers are used by aeronautical engineers when they design the airfoils (“wings” to ordinary people) of modern airplanes. Fact: The very planes we ride in to get from Boston to San Francisco or from New York to Miami have the correct shape because imaginary numbers are sometimes used as part of the aeronautical engineer’s mathematical toolbox when he computes the best wing for a given plane.
Question: The above statement being true (and it is), which is more important: that the wings of our aircraft have the optimum design OR that all numbers must be locatable on the number line?
Now doesn’t that question seem silly? Does the engineer care if a number can or cannot be found on the number line? The engineer is (we hope) a practical person. He is not (usually) philosophizing while on the job. He just wants results. He is designing wings. If he is a sensible engineer, he will use the numbers that assist him to achieve the best possible wing design with the minimum use of resources, time and effort. Therefore, he will usually use imaginary numbers.
Bluntly, useful numbers need not be members of the family of real numbers. So what would be a sensible, easy to comprehend and scientific criterion of a useful number? Let’s start with
“DOES IT WORK?”
When imaginary numbers are used properly and at the right time to solve a real-world problem, is the result constructive? Is our survival enhanced in some way by the application of imaginary numbers to the solution of a bona-fide, honest-to-goodness human problem or situation?”
The answer to the above questions is “Yes, we are much better off because of the existence and use of imaginary numbers.”
So, dismissing or ignoring or invalidating or rejecting imaginary numbers because they do not belong to the real number category and because they do not have all the properties of real numbers is an arbitrary.
Happily, imaginary numbers do retain many of the properties of real numbers – enough to allow real numbers and imaginary numbers to “cooperate” for the greatest good. For example, you can add, subtract, multiply and divide imaginary numbers.
BUT IF IMAGINARY NUMBERS CANNOT BE LOCATED ON THE NUMBER LINE, THEN WHERE, OH WHERE, ARE IMAGINARY NUMBERS?
I remember the first moment when I read in John Saxon’s Algebra 1 that any number is firstly and fundamentally an idea. At that time, this was an entirely new concept to me, and I was struck by its simplicity and truth. Saxon was right on the money. {John H. Saxon Jr. Real numbers and the Number Line. In Algebra 1. Nancy Warren (editor), second edition, pages 19-28. Norman, Oklahoma: Saxon Publishers, Inc. 1990.}
So, if an imaginary number is not graphable on the common number line, where is it? Is it only an idea? Yes, sort of…but no, not only an idea.
I answered that question for myself, so the following is simply my opinion. My personal conclusion is that an imaginary number’s location is the actual physical universe place where it is being used. Although imaginary numbers cannot be found on the number line, they do exist in the physical universe – in addition to being ideas in the minds of those engineers and scientists using them.
That means, literally, where is someone using one or more imaginary numbers to get a practical result? In what lab or factory? Appearing on what computers monitor? Where and in what diagram or rectangular coordinate system?
Written down in whose math worksheet? In whose mind is it part of a computation? In what computer’s memory is it being stored and manipulated by strings of smart 1’s and 0’s that were programmed by smart programmers?
What is its specific application? That’s where imaginary numbers are. So you might say they are everywhere people are using them or have used them or will use them. (Gee, that’s at least as many locations as are on the number line!)
Let’s see how this works. Here are three examples of imaginary numbers:
Each of the above expressions contains the square root of a negative number and therefore cannot be found on the number line.
However, imaginary numbers do follow some familiar rules used with real numbers. Like any square root, imaginary numbers can be simplified by using the Product of Square Roots Rule:
The square root of a product can be written as the product of the square roots of the factors of the product.
Using the above rule, the simplifications of the above imaginary numbers are:
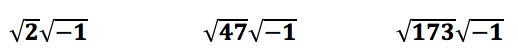
To make writing and calculating with imaginary numbers even simpler, a forward-thinking Swiss mathematician named Euler designated the letter “i” as the symbol for the square root of negative one.
To the uninformed observer, Euler’s use of “i” may seem like a big, fluffy nothing, but this symbol works so darned well that mathematicians, engineers, physicists and others who use a lot of math in their daily work have all agreed that
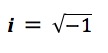So, in math, when you see the symbol realize that you are looking at an imaginary number. Imaginary numbers will almost always have an in them.
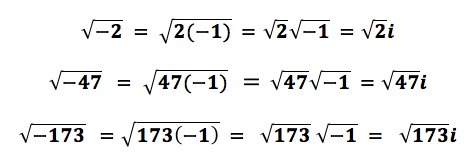
(Note: An exception can be found in electrical engineering, where the letter “j” is often used to represent an imaginary number instead of the letter “i” because “i” has a different, well-established meaning in electrical engineering.)
The advantages of using i are significant. Its use allows us to work with the square roots of all negative numbers simply and accurately. Performing the arithmetic operations on negative numbers is simplified by using i.
A UNIQUE PROPERTY OF IMAGINARY NUMBERS:
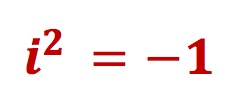
An imaginary number has a peculiar but useful property.
Once again, we’ll start with the definition of a square root for real numbers:
THE SQUARE ROOT OF A GIVEN NUMBER IS THAT NUMBER WHICH WHEN MULTIPLIED BY ITSELF EQUALS THE GIVEN NUMBER.
Thus, both 4 and -4 are the square roots of 16 because 4 x 4 = 16 and -4 x -4 = 16.
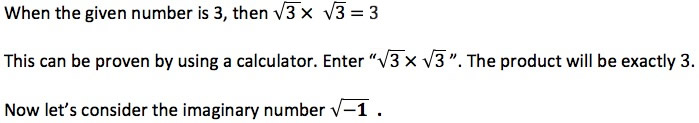
While holding our breath, we’ll use the same definition of a square root (for real numbers) and see what happens to our imaginary number:
Negative one (-1) can be found on the number line. It is therefore a real number.
The imaginary number is gone! (At least to me, that qualifies as pure MathMagic!)
(Note: The above calculation must be done by hand. It does not work in scientific calculators that use an algebraic operating system. Such devices only calculate with real numbers, not imaginary numbers.)
Some math authors use this property as a definition of an imaginary number:
DEFINITION #2: AN IMAGINARY NUMBER IS A NUMBER WHOSE SQUARE IS A NEGATIVE REAL NUMBER.
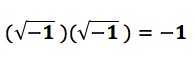
And since i x i can be written as i²
then i² = – 1
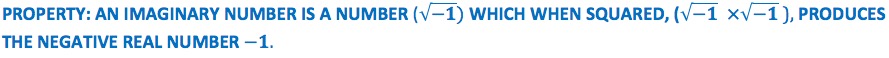
This property proves itself by being really useful when making real-world calculations with imaginary numbers.
The Future of Numbers
∞ PART FIVE ∞
A WINNING MATH TEAM
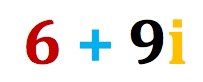REAL AND IMAGINARY NUMBERS WORK
TOGETHER IN THE FORM OF COMPLEX NUMBERS
BACKGROUND
DEFINITION: A QUADRATIC EQUATION IS A POLYNOMIAL EQUATION
WITH ONE VARIABLE IN WHICH THE HIGHEST POWER OF THE VARIABLE IS 2.
Some historical background is useful here. About 500 years ago, mathematicians were solving quadratic and other, higher degree polynomial equations. Some of these equations had “sensible” solutions — recognizable and useful solutions. For instance, the quadratic equation
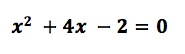has two real number solutions:
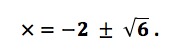
Occasionally, however, solutions appeared that the mathematicians did not understand. For example, the solution to the quadratic equation
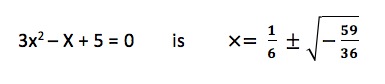
Earlier mathematicians might have simplified this solution to
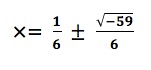and perhaps simplified even it further to
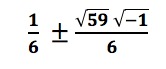
But that’s all they could do. The solution still contained the square root of a negative number:
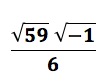Understandably, they had no idea what it meant or what to do with it because such numbers could not be applied to any of their real-world problems.
In the 17th century, after much research and dispute, Descartes (a math genius in so many ways — but he sure missed on this one!) called them “imaginary” numbers as an insult and the name stuck.
(By the way, there was no “set of real numbers” before Descartes. There were just “numbers”. Descartes invented the name “real numbers” to distinguish them from the “imaginary numbers” he rejected.)
That sad event occurred long ago when mathematicians, physicists and engineers had no knowledge of supersonic jets, electronic circuits and computer graphics.
DEFINITION OF A COMPLEX NUMBER
The word “complex” is sometimes used with the meaning: difficult to understand. But there is another definition of complex: involving a lot of different but related parts. And that’s exactly what it means in the term “complex number.”
Mathematicians, physicists, engineers and other scientists have learned that imaginary numbers are most useful when combined with real numbers. So, to describe the applications of imaginary numbers in the real world, we first need to know about the complex number.
DEFINITION: A COMPLEX NUMBER IS A SINGLE NUMBER THAT COMBINES BOTH REAL AND IMAGINARY PARTS.
We can generate a complex number by solving the quadratic equation 3X ² – X + 5 = 0 using the quadratic formula or by completing the square.
THE STANDARD FORM OF A COMPLEX NUMBER:
In the same way that mathematicians have agreed upon a “standard form” for a linear equation (ax + by + c = 0), and a quadratic equation (ax ² bx + c = 0), there is a standard form for a complex number: a + bi. By agreeing upon “standard forms” for various expressions and equations, all mathematicians and math students “are on the same page” and can communicate mathematically and work together cooperatively.
STANDARD AND NON-STANDARD FORM SYMBOLS
FOR COMPLEX NUMBERS
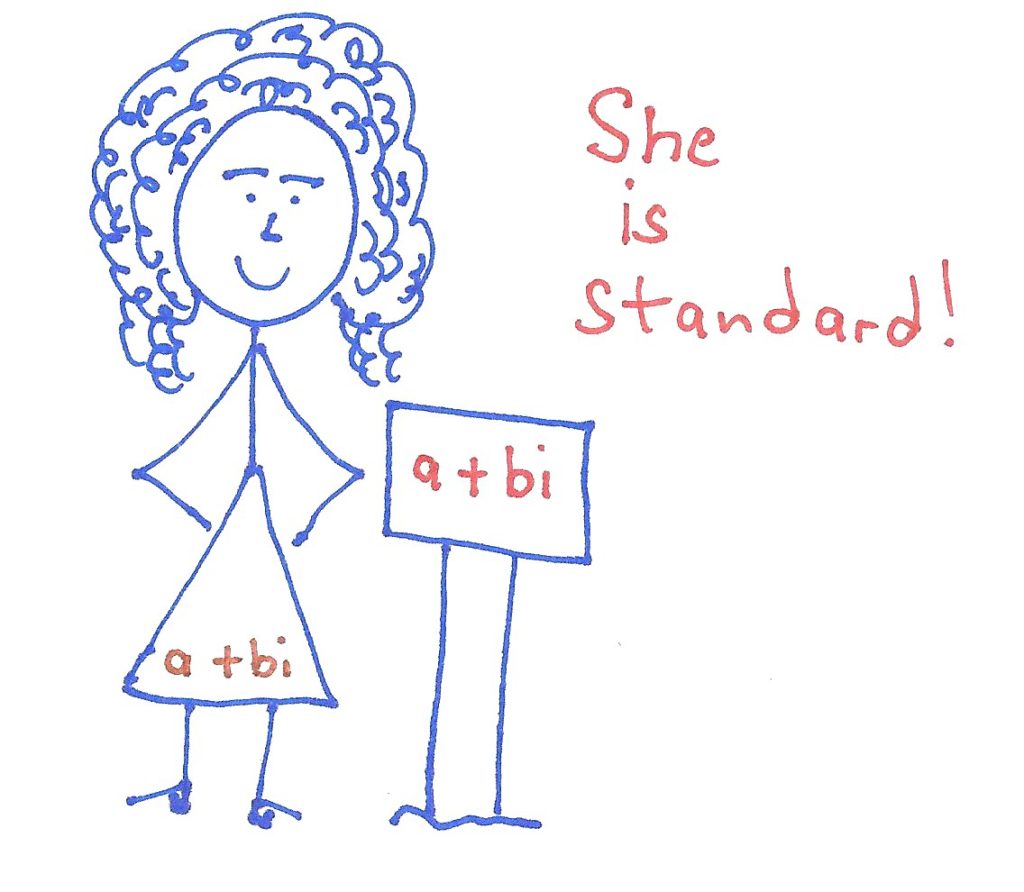
The small letter “a”, as a variable, represents any real number.
The small letter “b”, as a variable, represents any real number and is the coefficient of i.
If we write the real part of a complex number first (“a’’) and the imaginary part second (“bi”), we have written a complex number in standard form.
All of these numbers are complex numbers in standard form:
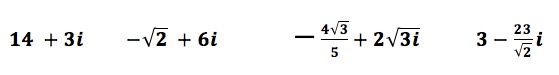
The Future of Numbers
∞ PART SIX ∞
BUILDING A REAL WORLD
WINNING MATH TEAM
APPLICATIONS OF IMAGINARY AND COMPLEX NUMBERS
An Algebra 2 student researching the subjects of imaginary and complex numbers runs head on into this fact: a full understanding of any application of imaginary and complex numbers—and there are a great many—requires great familiarity with complex math and science that is learned only in advanced physics, biology, chemistry and statistics courses. In other words, the knowledge required to really grasp their actual use is not available to most Algebra 2 students and is attainable only at the college, university or post-graduate level.
But, given that limitation, many applications of imaginary and complex numbers can be described in a general way.
It should be noted that complex numbers do not usually replace real numbers. For example, in doing circuit design, the electrical engineer can often (but not always) use real numbers for his circuit design work if he chooses. However, since he can do the same task better and faster using complex numbers, he will use complex numbers for certain tasks. This situation is typical of the use of complex numbers: they usually do not replace real numbers but they are often a better mathematical tool than real numbers used by themselves.
ELECTRICAL ENGINEERING
Complex numbers are used heavily by electrical engineers involved in circuit analysis and design because complex numbers simplify finding solutions to their problems. In particular, they simplify the analysis and control of alternating current signals (alternating electrical signals continuously change direction, first flowing one way on a circuit, then reversing direction and flowing the other way on the same circuit. This reversing pattern repeats as long as the alternating current is on.)
PHYSICS
Physicists use complex numbers when analyzing electromagnetic field strength. An electromagnetic field is the energy field generated by electromagnetic waves, which include such common waves as radio waves, microwaves, visible light (red, orange, yellow, green, blue, indigo and violet), ultraviolet waves, X-rays and others. All these waves have two distinctly separate components: an electrical aspect and a magnetic aspect. Rather than trying to describe an electromagnetic field mathematically by means of two real quantities (one real number to measure the electric field strength and another real number for the magnetic field strength) it is best described by a single complex number, of which the electric and magnetic components are simply the real and imaginary parts.
SOFTWARE DESIGN AND ENGINEERING
For those who create art with computers, complex numbers are used in writing the software that generates a kind of computer graphic called “fractals.” Fractals are geometric objects that are created by making a pattern repeat many times.
AERONAUTICAL ENGINEERING
As mentioned earlier, complex numbers are applied to studying the flow of air over airplanes at high speed. For example, an aircraft’s wings are designed using complex numbers.
CIVIL ENGINEERING
Civil engineering is the branch of engineering concerned with the planning, design, construction and maintenance of such things as roads, bridges, and dams. Civil Engineers use complex numbers while designing and testing the strength of bridges.
ARCHITECTURAL ENGINEERING
(Architectural engineering, also known as building engineering, is the application of engineering principles and technology to the design and construction of buildings.) Complex numbers are used in the analysis of stresses on the structural beams used in buildings.
Also in architectural engineering, complex numbers are applied to the study of resonance of structures. (In physics, resonance is the effect produced when the natural vibration frequency of a body is greatly amplified by vibrations at this same frequency from another body.)
AUTOMOTIVE ENGINEERING
Complex numbers are used when analyzing the movement of shock absorbers in cars.
MECHANICAL ENGINEERING
Mechanical engineering is the branch of engineering that involves the design, production, and operation of machinery.) Complex numbers are used during the design of dynamos and electric motors. (A dynamo is a machine that generates electricity.)
AUDIO ENGINEERING
Engineers who design speakers use complex numbers.
ENERGY STORAGE
Scientists and engineers who run experiments on ways to make and store energy using batteries and solar energy systems use complex numbers.
QUANTUM PHYSICS
The mathematically-based physics pioneered by Isaac Newton reigned supreme in the physical sciences until the end of the 19th century. At that time, it was observed that matter and energy at the atomic and subatomic level behave very differently than matter and energy at our normal, everyday, human-eye perception level. For example, the equations derived from Newton’s three Laws of Motion were unable to make accurate predictions of location, path and velocity of very small particles, even while the same equations were accurate in our everyday universe. Simply stated, Newton’s Laws of Motion simply failed to work when applied to really small stuff.
This failure of Newton’s physics required the development of a new physics. This new theory, introduced in 1900 by Max Planck and developed by many other scientists since then, is called “quantum theory”. Quantum theory (and the math used in that theory) succeeds in accurately describing what actually happens to the really small particles of energy and matter.
When scientists are working in the field of quantum physics, real numbers (all by themselves) are inadequate to supply the math needed to describe some conditions at the atomic and subatomic level. Quantum physics requires extensive use of imaginary and complex numbers. In other disciplines (such as the engineering specialties listed above) there are often ways of making calculations that do not require complex numbers. This is not the case with some of the math used in quantum physics. Here you sometimes either use complex numbers for certain calculations or you do not calculate! (Complex numbers in quantum mechanics, https://courses.physics.illinois.edu/phys580/fa2013/susy_v2.pdf)
The knowledge and discoveries born out of quantum theory led directly to the invention of the laser, the electron microscope and the transistor. The development of modern computers, smart phones, etc. was made possible by quantum theory.
The Future of Numbers
∞ PART SEVEN ∞
MATH IN THE FUTURE:
NEW NUMBERS WITH NEW PROPERTIES
LESSONS TO BE LEARNED
The history of the physical sciences and mathematics demonstrate that progress is often a bumpy road. Science has not always moved upwards on a smooth path with every scientist and mathematician understanding and appreciating the new discoveries that eventually were used to advance the knowledge and survival level of mankind.
Within the mathematical field of numbers, the discovery of irrational numbers by the ancient Greeks and, much later, the use of negative numbers were both originally met with considerable confusion, skepticism and outright rejection. Now, of course, irrational numbers and negative numbers are commonplace, accepted and widely used even by middle school and high school students, as well as the army of engineers, mathematicians and scientists who depend on them for the accuracy of their daily work.
Imaginary and complex numbers are just newer examples of this same cycle of discovery, rejection and ultimate acceptance when the phenomena uncovered are found to increase our understanding and control of the physical universe.
Given mankind’s documented history for discovering and/or creating new and useful mathematical tools that have provided us with greater and greater control of the physical universe, would it really be so surprising if current and future mathematical researchers, while attempting to uncover further hidden properties from the “measurable”, (the purely quantitative aspects of our universe) bring to light New Numbers with New Properties?
I envision mathematicians, physicists and other scientists (both amateur and professional) uncovering NEW NUMBERS with NEW PROPERTIES that prove to be just as useful as the set of numbers we call “real numbers” — and as useful as imaginary and complex numbers — and then, eventually, applying these New Numbers with New Properties to achieve practical ends.
NEW NUMBERS WITH NEW PROPERTIES
In keeping with the possibility (likelihood, actually) of new numbers being discovered or created, I propose designating those new numbers that will be found “somewhere or anywhere” to be
NEW NUMBERS WITH NEW PROPERTIES.
Such a name would, of course, be instantly abbreviated to just New Numbers and then further abbreviated to NN. (But even NN — italicized, of course — has a nice ring to it!)
But without the number line, how do we orient ourselves with regards to New Numbers with New Properties?
THE ANSWER IS BY MEANS OF REAL-WORLD APPLICATIONS.
The question “Where is New Number XYZ?” is answered by “How will NN XYZ be used? What practical purpose does it fulfill right now? Where do we start applying NN XYZ to the world of people, mountains and bees (and dirt-cheap, renewable sources of energy and black holes and faster-than-light starships and….”)
If no current purpose can be found, we still do not discard, ridicule or smash New Number XYZ. We carefully and respectfully place it in a bin labeled:
“Reserved for New Numbers with New Properties that have no immediate applications. Hold indefinitely for mankind’s future.”
THIS IS A VERY SPECIAL NUMBER BIN!
RESERVED FOR NEW NUMBERS WITH NEW PROPERTIES THAT HAVE NO IMMEDIATE APPLICATIONS. HOLD INDEFINITELY FOR MANKIND’S FUTURE.
If such NEW NUMBERS WITH NEW PROPERTIES have an appropriate name and category to be part of, perhaps they will be warmly welcomed, validated and more rapidly applied to helping mankind increase its survival rather than becoming the subject of just another sad event in that dull series of jealousies, arguments and wasteful controversies that have occasionally marred the history of scientific advance.
the end
Copyright © 2016, 2017 Bruce Silton
A MESSAGE FROM THE AUTHOR
Has the information in this paper helped you understand imaginary and complex numbers better (as well as my Theory of Math Holes)? Do you have question, comments, or ideas of your own? You can write to me by using the contact page on my math educator’s website:
www.MathCreativity.com
or my artist/designer’s website:
www.BruceSilton.com
ABOUT THE AUTHOR
Bruce Silton is a tutor at Clearwater Academy International, a preschool–12th grade private school in Clearwater, Florida. Since March of 2000, he has delivered approximately 17,000 tutoring sessions to students of all ages. Some 10,000 of those tutoring sessions have been devoted to helping students overcome difficulties learning math.
Math editing by Ardiana Radani
English language editing and proofreading by Leslie Silton, Book Doctor
(I added considerable material to this paper after Leslie and Ardiana completed their editing. Therefore, I take full responsibility for any errors in both English and math.)