LIVING WITH MATH

Real-World Applications for Primary
and Secondary School Mathematics

by Bruce Silton

Copyright © 2016, 2017 Bruce Silton

Acknowledgments

The basic concepts for this paper did not spring into my mind from nowhere. Among the many individuals whose thoughts contributed to this work, two stand out.

Many years ago, Jim Zwers, the Executive Director of Clearwater Academy International, introduced me to his concept of a “goals-oriented education”: the firm principle that an education, to be truly effective, must be related to a student’s own goals.

L. Ron Hubbard’s study methods and philosophy of education have influenced and enhanced every aspect of my work with children. This paper on providing our students with real-world applications for each major topic in their math courses would not have been written without his help.

Bruce Silton
Pinewood Village
December 20, 2016

Note: Naturally, as an author, I accept full responsibility for the ideas expressed in  “Living with Math.” The concepts and practices described in this paper are, ultimately, my own and not necessarily those of my school, its faculty or curriculum.

Living With Math

∞ PART ONE ∞

THE IDEAL ROAD IN AN IDEAL WORLD

The Ideal Road in an Ideal World

The ideal road for producing lots of powerful math kids is paved with real-life applications for every major math topic taught in primary and secondary school mathematics from 1st through 12th grades.

And to be wholly effective, study materials teaching real-life applications must be close at hand so that students actually use them while they are studying their math lessons.

A teacher should be able to ask a student how he, as an individual, is actually going to use what he has just learned and get a meaningful answer. If he can’t get an honest reply that directly connects that specific math topic to his current and future life, then that student is to some degree at risk of losing interest in the subject of mathematics. If he then, over time, mentally accumulates enough topics for which he has little-to-zero use, he will all-too-often withdraw from the entire subject while singing the familiar melody and lyrics of exasperation: “I hate math! Boring!” And with that withdrawal goes any possibility for either career or avocation that depends upon literacy and competence using the language of mathematics.

The problem stated in the paragraph above is not hypothetical. It IS what happens to many students.

The solution? The math student should know how every major topic he is studying will be used in real life, and he should know that application as he is studying the subject, not later. Further, he should know how that topic applies specifically to him.

If these conditions are not met, we will continue to add to the throng of math-illiterates and semi-illiterates, all to the detriment of the individual himself and the groups to which he belongs.

In an ideal world, all math textbooks would contain an abundance of easily-understood, compelling, real-life applications for each math topic presented in that textbook.

The very best math books already provide students and teachers with some specific uses, but, since math texts tend to be long (and the school year short), such applications are ordinarily not presented with sufficient depth, detail, drama, aesthetics, and exercises to truly involve and excite the interest of the students.

Other texts state mainly the unadorned technical concepts with only an occasional, casual mention of how the math is used. Such books, being light on application, force teachers and students to research for real-life uses, which research (because of the time and effort involved) is often not done. This situation leaves enormous gaps between book learning and real-world use.

The Solution

First, a comprehensive series of books dedicated solely to providing real-life purposes and applications for every major math topic taught from 1st through 12th grades.

and

Second, a series of internet videos, created in intimate partnership with the book series and sharing the same title, purpose, and general content.

This paper describes the essential features of both the proposed book and video series. Each concept and guiding principle described herein is equally valid for both paper and digital format. The differences between the book and video forms of Living with Math (LWM) will, of course, be those dictated by the inherent and unique qualities of two such distinct modes of expression.

The widespread lack of strong interest in mathematics and the general failure of so many of our young people to learn and apply it in their day-to-day lives (beyond a passable competence using the four operations of arithmetic) emphasizes the importance of both forms of LWM (books and videos) being available for educators as they strive to achieve math literacy and competence for the greatest possible number of students.

A Future to be Created

The comprehensive book and video series described in this paper, Living with Math: Real-World Applications for Primary and Secondary School Mathematics, does not yet exist. It is an idea in my mind. But it should exist because the teaching/learning methods and materials described in this paper are needed right now. This paper, then, is an offer and a call to those individuals and groups who have a strong and continuing interest in creating a future of math literacy for the greatest possible number of individuals.  To be of use to educators and students, the idea must be carried out — actually created, polished, published, and distributed. Individuals and groups who would like to lead or assist with the implementation of LWM are invited to contact the author, Bruce Silton, using the contact page at www.MathCreativity.com.

The Core Concept

The driving concept behind Living with Math (LWM) is straightforward and down-to-earth: to give primary and secondary school teachers and their students a comprehensive, illustration-rich source book and video series containing a minimum of five (more is better!) informative, detailed, visually arresting REAL-LIFE applications for each one of the main math topics found in the standard Arithmetic, Pre-Algebra, Algebra One, Geometry, Algebra Two, Trigonometry,  Pre-Calculus and Calculus textbooks used in primary and secondary schools.

Bridging the Gap With
Easily Doable Exercises

While math teachers understand the direct connection between math competence and the student’s successful navigation through the technologies of 21^st Century life, students often do not. This connection has to be intentionally brought home to them. Therefore, LWM must also supply enough easily doable exercises and projects to be completed by students so that they wind up being competent at solving not only academic exercises but using math topics as tools to solve some of life’s actual problems.

A hastily compiled list of such doable problems-to-be-solved will not do. There is a way to do this right: each problem should be considered as a preparation for life. Individual problems must be presented in a series of small, easily doable steps. Each and every step should be explained fully and logically justified, with no steps omitted “because the student is supposed to know them already.” The student  does the steps of the problem to a proud completion.

Further, once a student has mastered the individual steps needed to solve such simple, real-life problems, he should repeat the solution of each problem in full with all steps executed perfectly until he can do it at speed. This process of repeating all the steps of the solution at speed goes quickly. Although it adds very little time to the lesson, it has an extremely important, positive impact on the student’s confidence and competence. He is, in effect, DRILLING the individual problem until it is not just solved correctly but solved correctly and FAST. When this result has been honestly accomplished, that student has achieved certainty and can be considered safe to continue on to the next and final step in his Living with Math program for that topic.

The Final Step: Creating Problems

Because Life (after one graduates) does not always present one with well-thought-out, neatly-printed problems to solve, students must be trained to perceive (in the midst of the drama and motion of living life) the existence of a problematic situation that needs, at least in part, a mathematical solution. This requires an ability rarely taught or learned in our primary or secondary schools: the ability to create, state, solve, and check one’s own problems while demonstrating understanding of the words and solutions involved in the self-created problems (but only those words and algorithms appropriate to the student’s grade level). ALL THIS MUST BE ACHIEVED WITHOUT REFERRING TO HIS TEXTBOOK OR TEACHER.

I have developed a precise, workable, teaching technology devoted solely to the creation of math problems by students. The teaching method is written down in useable form in my paper “The Other Side of Math”, another page on my website, www.MathCreativity.com.

Until a student can easily create, state, solve, and check his own problems with understanding, he is not done with a particular topic in LWM. It is further noted that this ability is rather easy to attain once one can solve at speed the exercises for that topic presented in LWM.

Living With Math

∞ PART TWO ∞

ORDERS OF MAGNITUDE

Definition of Order of Magnitude:

Definition: If something is ONE order of magnitude greater or smaller than something else, it is 10 times greater or smaller in quantity (size, number or amount). If something is two orders of magnitude greater or smaller than something else, it is 100 times greater or smaller in quantity. The next order of magnitude (three) would be 1000 times greater or smaller. And so on, each time getting ten times greater or smaller than the previous one.

The importance of providing real-world applications of math topics for primary, middle, and high school students is well-understood by most modern educators. On this point there is no longer any serious disagreement. Gone are the days when it was acceptable to stuff kids with abstract ideas for which they were given no or minimal connection to the world of people, bees, mountains, and trees.

But it is the order of magnitude of quantity and quality required to fill the need for applications in a form that truly communicates and inspires young students to learn — and motivates them to continue learning — that has been missed.

An in-depth search of libraries, bookstores, and the Internet will bring to view many presentations of real-world math applications in book and video form. Some are excellent and some are not. But nowhere will you find in one place, in one complete series of books and videos, the applications — not the algorithms or axioms or solutions but real-world uses — for every major math topic taught in 1st through 12th grades. And not just one application for each topic, but a range of them (preferably five or more) that will reach, appeal to, and encourage the widest possible number of students.

Why, one might ask, would such a wide range of applications be necessary? Why not one application per topic? Because, as every teacher knows, young people do not dream the same dreams. It is unique, passionate purposes that impel individuals through life and motivate them to gain knowledge and overcome the inevitable barriers encountered on the way to becoming successful in any field of endeavor.

While good teachers know how to find a student’s purposes and set them on fire, the fact is that there are literally billions of students and each one needs to achieve math literacy. Given that math classes are usually too large and (relatively) that math teachers are too few, how does a teacher light the dreams of 20, 30, or more unique kids while trying to teach 100 or more major topics per year? Obviously teachers need effective help. LWM will provide that help but only if the books and videos actually reach right inside a boy or girl’s intimate, personal universe, and fire up that young person’s own purposes.

Such a degree of stellar communication and penetration cannot be accomplished by presenting only one way to apply a topic. And it certainly cannot be accomplished with mediocre presentations.

Reaching Inside the Individual Student

So, what real-world application could make decimal fractions truly interesting to a 4th grader? Well, it would depend entirely on that particular 4th grade student’s purposes for his or her life. Some boys and girls brighten up at the idea of becoming a Special Forces soldier. Others are excited by handling money in the world of banking and investing. Religious goals and charitable ideals motivate others. Still others will want to compose and perform music — or dance and act or make others laugh or design skyscrapers or develop video games or be a great mother and raise four terrific kids or teach elementary school to neglected children or be an investigative journalist or write compelling murder mysteries or invent a faster-than-light drive for starships or…the list of possible purposes is very long indeed! To succeed, then, LWM must connect the topics of math to the greatest possible range of interests.

To be blunt, if we think we will reach a wide range of students with one application and operate with that belief, this program will surely fail, for it will exclude the greatest number of students. On the other hand, a complete set of LWM books and videos that present an adequate, well-surveyed range of real-world uses will, if available in every school to every teacher and every student, bring about a renaissance of REAL learning in the science of mathematics.

Without exception, every math student, starting with one-digit addition in 1st grade arithmetic and continuing on up until he or she graduates high school, should have the use, the purpose, the real-world application of every major topic as he studies that topic. Consider the order of magnitude of learning that will be created by twelve unbroken years of topic-application, topic-application, topic-application, etc. There will be no gaps. There will never be a time when a student is left wondering, “Hey, teacher, what am i ever going to do with this stuff?” It won’t matter if he is learning to borrow across 3 zeros in subtraction (3rd grade) for the first time or solving problems of indirect variation squared by finding the constant of proportionality (9^th grade), he will know why it exists, why he is learning about it, and how it might apply to his life.

Therefore, to produce the LWM series of books and videos with an adequate quantity and quality of real-world applications will be an enterprise at least one order of magnitude greater than any publishing program that has heretofore been attempted or produced in the field of math education. If the order of magnitude of investment in terms of leadership, devotion to the mission, intelligence, time, art, and money that will be required to design, produce, and bring to market LWM is understood, accepted and planned for at the outset, this publishing program will be enormously successful in achieving its goals.

What Is a Major Topic?

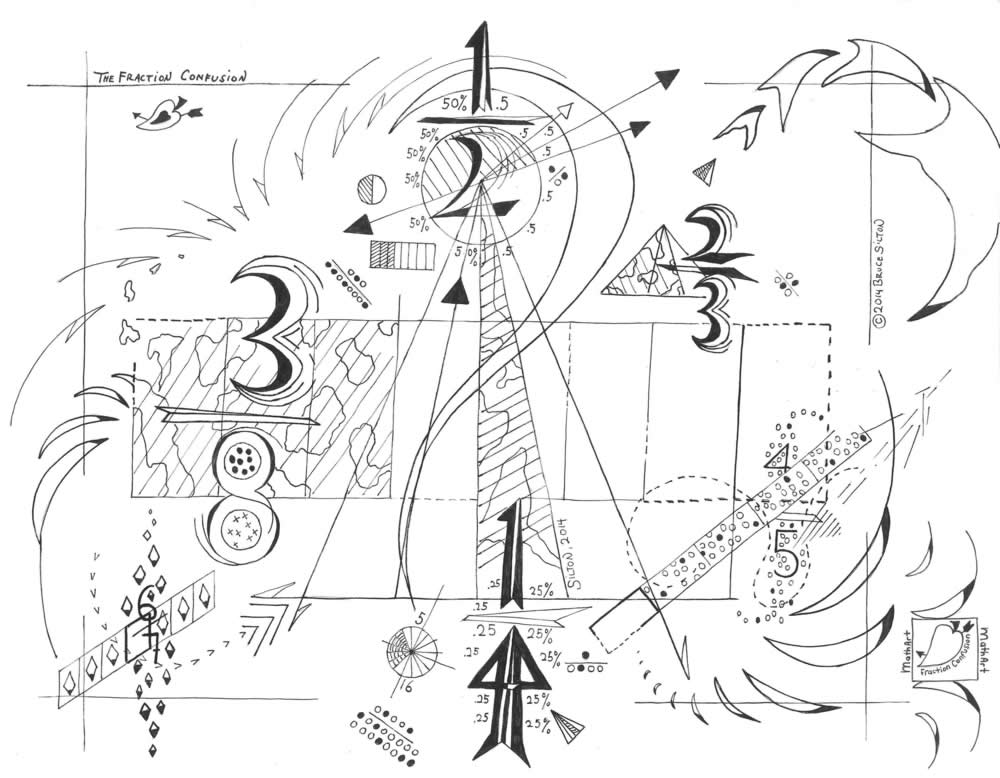
Now, let’s name and examine for relative importance each separate topic from one typical unit (out of 11 total units) of a 3^rd grade math textbook (Thoburn, Tina, Forbes, Jack E., and Bechtel, Robert D. Mathematics, New York, Macmillan Publishing Company, 1985) to determine which ones could be considered “major” (and therefore requiring inclusion in LWM) and which ones can be neglected. (The topics are in order of presentation in the textbook):

Fractions of a whole thing

Equivalent fractions

Comparing with fractions (using number lines and the symbols <, > and =)

Fractions of sets

Fractions of numbers

Fraction word-problems

Mixed numbers

Decimal fractions expressed in tenths

Decimals greater than one (mixed numbers)

Decimal fractions expressed in hundredths

Adding and subtracting with decimals (including money and regrouping to hundredths)

Decimal word-problems to hundredths

Measuring with centimeter rulers

That’s 13 topics in just one chapter out of a total of eleven chapters. Which of these topics are “minor” and not deserving of their own place in the understanding of an 8-year-old math student? Which ones will he not need in his 4th, 5th, and 6th grade study of math? Which ones will a boy or girl never need to understand and apply in order to be successful in accounting, music, computer science, engineering, architecture, construction, automobile design and mechanics, electronics, genetics, banking, aerospace, medicine, nutrition, the military or government? Which ones will not appear in his pre-algebra and algebra lessons? And, finally, which ones would you want neglected in the education of your own children? These questions answer themselves: each of the above topics is an integral element of the language of mathematics. Each one is part and parcel of the mathematical language that permeates the work-a-day world of the 21st Century.

Factually, Earth’s production and communication lines literally “buzz” with ideas and terminology that directly or indirectly use each topic listed above – and, one way or another, EITHER INDIVIDUALLY OR IN COMBINATION WITH OTHER TOPICS, all must be included in the LWM series of books and videos.

Building the Living With Math Library
Step by Step

Regardless of good leadership, adequate facilities, proper funding, great illustrators, writers, curriculum developers, and all the other necessary publishing resources being available in abundance, LWM will not become a completed reality overnight. Any major, worthwhile, educational publishing program takes time to develop from initial conception to published/marketed reality. Well, LWM is bigger than any math program that precedes it, and it, too, will require time to develop.

But that does not mean the entire LWM library must be completed in full, with all topics covered for all grades from 1st through 12th, before the books and videos can be used in classrooms. On the contrary, one grade at a time can be completed, published, marketed, sold, and put into classroom use while the book(s) and videos for the next grade are being developed. In this way, real help can be given to schools and their students and income can be earned by the publishers while the applications for the next grade are being created.

When produced in this step-by-step manner, LWM should be developed from the bottom up. That means 1st grade first, 2nd grade second, 3rd grade third and so on all the way up the ladder to twelfth.

Why start from the bottom up? Because we lose tons of kids right at the starting gate — so let’s stop the losses and build more powerful math kids from the very first time our 6-year-old boys and girls open to their first lesson in their 1st-grade math textbook.

Purposes

Each and every topic in math has two distinct purposes.

The first is the general use of that topic: Why was it developed? What typical real-life condition or situation was it intended to handle? Probably it was meant to solve a common problem in the real world, but what? What overall result or goal will be achieved when that particular math algorithm is correctly applied? This broad purpose will be found valid in a general way for almost everyone.

But simply knowing the overall purpose for a topic rarely lights a fire inside our young math students. And, to achieve ultimate success, you must light the fires of learning.

This truth leads directly to the second purpose, the individual application of that same math topic to a particular student’s life: How is Joe or Mary going to use ______ right now, outside of the classroom or school? How might it be used in that student’s future? As an adult? In a career? And how could this math relate to his survival?

When you can bring a student to life on these two purposes, you have a student who will expend the necessary thought-muscle (mental effort) and thought-energy (reason or rationality) to learn and apply that math.

Thus, the publisher, producers, editors, authors, and illustrators of Living with Math have two overriding purposes:

1) TO MAKE EVERY MATH TOPIC VIVIDLY REAL BY REVEALING ITS OVERALL USE IN LIFE.

2) TO GIVE TEACHERS ENOUGH REAL-LIFE APPLICATIONS PRESENTED IN A STELLAR MANNER SO THAT THEY CAN CONNECT UP ANY ONE MATH TOPIC TO THE PARTICULAR LIVES OF THEIR INDIVIDUAL STUDENTS.

If they succeed in these two tasks, they will have succeeded.

How Teachers Can Use Living With Math

This twin series of books and videos is definitely not conceived or intended as a substitute for standard math textbooks used by students to actually learn a topic. With the expert guidance of good teachers, good math textbooks and teaching videos are pure gold. They are used to TEACH students the specific math topics, whereas LWM has two different uses. First, it is intended to be used consistently and methodically with each new math topic as a vital extension to the material in the student’s everyday text. Thus, when 5^th grade teachers and their students turn to this compilation of purposes and applications, it is assumed that they have just learned from their regular math book the theory and mechanics of, for example, locating points on a coordinate graph or dividing by a decimal number or using percents to name part of a group. LWM would then be used to provide an abundance of uses for those skills and thereby complete the learning process.

Secondly, it would provide a remedy when a lack of adequate applications in the students’ classroom textbook is actually stopping students from learning a new topic. Factually, students do not learn well when they do not personally see an actual use for what they are supposed to be learning. Yes, they may be able to memorize some rules and, yes, they may be able to repeat back a solution procedure, but they do not really learn and they are unlikely to apply that material in their lives. The process of learning requires creative contribution from the student — and creative contribution derives from the individual’s very own purposes for his or her life.

Let’s say that a 7th or 8th grade student in a Pre-Algebra class is unable to move forward either in learning or retaining the definitions and rules for handling negative numbers because he is simply not interested in negative expressions. He thinks, erroneously, that they have absolutely nothing to do with him.

But by means of LWM, the student would be introduced to a selection of carefully chosen, illustrated, detailed, negative-number situations, ranging from minus checkbook balances caused by overspending to yardage penalties in a football match to undersea adventuring — to something truly heroic, like the combined below-zero temperature and wind-chill factors encountered by mountaineers during high-altitude expeditions.

Living With Math

∞ PART THREE ∞

QUALITY FIRST

QUALITY FIRST

The future publishers/producers/creators of Living with Math should understand clearly that the quality – the quality, not the quantity – with which applications are presented is the make-break of this concept.

The above illustrations of the digits 0 and 2 are included simply to demonstrate that the simplest, the most common concepts, symbols, axioms, definitions, theorems, procedures, and applications of primary and secondary school math, from the teaching of digits in 1st grade on up the mountain to Calculus at the top, can be accomplished with a high degree of aesthetics. Beautiful lines, forms, and calligraphy combined with exciting pictures and colors plus excellent prose are far more likely to create interest in students, to be perceived, and accepted by them than the mundane.

AESTHETICS PENETRATE MINDS BECAUSE THE MIND IS ALREADY ATTUNED TO RECEIVE PERCEPTIONS OF BEAUTY AND REJECT OR IGNORE THE COMMONPLACE AND THE UGLY.

Therefore, in order to connect the ideas, usefulness, and importance of mathematics to the broadest possible range of student minds, each and every application must be illustrated by powerful visuals, and expressed in simple, engaging, and persuasive language that is geared precisely to the age/literacy level of students learning that topic for the first time.

(My intention in emphasizing quality is not to diminish the importance of quantity because — one way or another, either singly or in combination — all major topics should be included in LWM.)

Aesthetic, vivid presentations of how the math applies to the real world will, in many cases, crack the “It has nothing to do with me” attitude held by so many young people — and by “vivid presentation” is meant visually arresting photographs, drawings, diagrams, tables, history, stories, and anecdotes of, for example, Sir Edmund Hillary and Tenzing Norgay (Hillary’s Sherpa guide) consulting their temperature gauge in the early morning hours of May 29, 1953 at their high camp (27,900 feet) while deciding whether or not to go for the top of Mount Everest, the planet’s highest peak.

If we then combine the above-narrative with uncomplicated, well-expressed basic data regarding the effects of extreme below-zero temperatures on human physiology in the “death zone”, a vital algebraic concept has a good chance of coming alive in the student’s mind.

The “death zone” is the name of the area above 8,000 meters/26,240 feet on some Himalayan mountains. At these heights, there is so little oxygen and such severe weather that a climber’s life, regardless of climbing hazards, is endangered simply by being up there. 

Now, having a degree of personal interest, the student will be far more willing to invest himself in learning, understanding, and applying negative numbers. The truth is that negative numbers are intensely real and, one way or the other, they do affect our lives. Furthermore, understanding them will surely open the door for students to attain higher levels of knowledge.

Exercises that teach raising a base to a power can be pretty dull to some 11-year-old boys and girls. But what if these same kids were drawn deeply into the world of earthquakes where they can discover the powers of 10 through the life and death drama of quake science — seismology?

Shouldn’t they find out about the Richter Scale,
not just with dry numbers but with real people and photo-stories?

And who was Charles Richter, anyhow, the American seismologist who developed the widely-used scale that bears his name? Providing details and anecdotes of a man’s life can make a whole subject come alive for students.

Richter, for example, was a sci-fi fan who adored Star Trek and avidly devoured other science-fiction works. For a period of time, this 24-7 seismologist actually kept a seismograph in his living room so he wouldn’t miss a significant quake! (“Charles F. Richter.” YourDictionary, n.d. Web. 28 October 2016 http://biography.yourdictionary.com/charles-f-richter>.)

Well, why was 10 used as the base number for calculations of quake amplitudes? Through his interest in the stars, Richter knew that astronomers used powers of 10 to calculate and compare the relative brightness of stars, galaxies, and other heavenly bodies. He translated the stellar (and interstellar) applications of exponential expressions to his earthy passion. (“Charles F. Richter.” YourDictionary, n.d. Web. 28 October 2016 http://biography.yourdictionary.com/charles-f-richter>.)

(The Richter Scale grows by powers of 10. An increase of 1 point means the strength of a quake is 10 times greater than the level before it. An earthquake registering 2.0 on the Richter scale is 10 times stronger than a quake registering 1.0. A quake registering 3.0 is 10 X 10 or 100 times stronger than a quake registering 1.0. A 4.0 is 10 X 10 X 10 or 1,000 times greater than 1.0 and so on.) (“Charles F. Richter.” YourDictionary, n.d. Web. 28 October 2016 http://biography.yourdictionary.com/charles-f-richter>.)

 Elaborating further, what events led up to the use of the seismograph? How does it work?

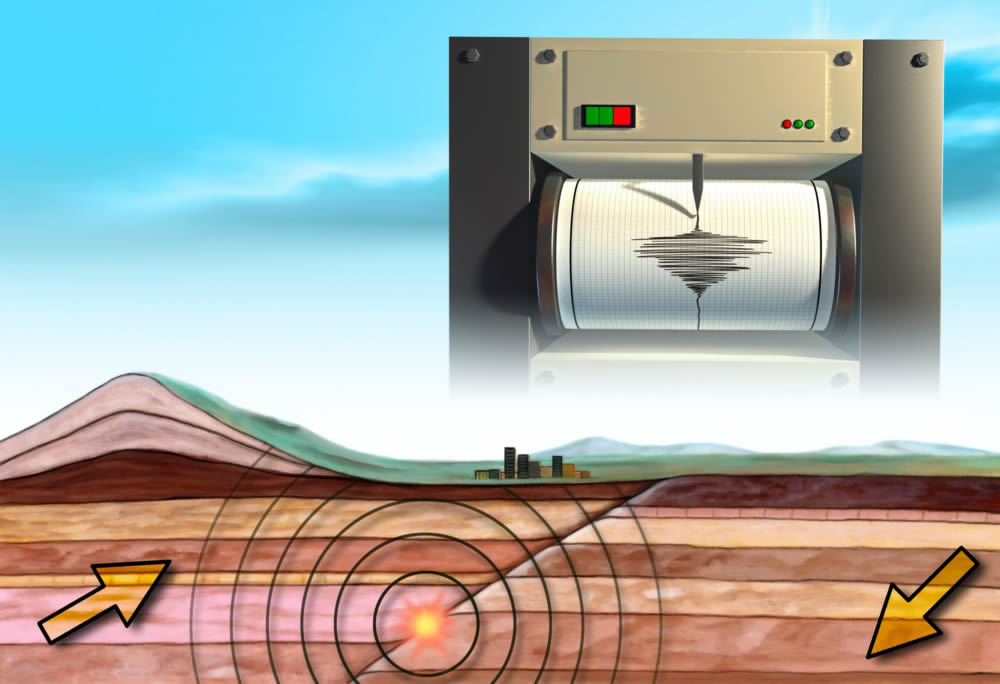
Using exponents both mathematically and graphically, how do you compare the strength and relative danger of quakes? Excellent, large-format photographs of actual events can communicate with power the relative differences between a 5.0 and a 6.0 quake. And how can this knowledge be used by people in Los Angeles, San Francisco or Tokyo?

So, if a textbook fails to supply a particular student with sufficient motivation to learn the raw math of a particular topic, LWM would be employed to supply an entire series of intensely real realities that draw the student into the topic. Once this is accomplished, the student (who now knows why he is learning and how it might relate to his current and future life), can suddenly take off and master the math in his textbook.

(Subjects more abstract than arithmetic will require additional research, imagination, and cleverness to be properly connected to the real world. See the section headed “Algebra and Beyond” later in this paper.)

Adding Dimension to Math

Student interest can be raised even further by comparing current applications to historical uses and postulated future applications. Whenever possible the names, dates, and stories of real people, groups and places where the data was, is, or will be used, are to be included — especially stories about the actual researchers/developers/disseminators of the math or its applications, always including enough curious, anecdotal details to demonstrate the drama and excitement of discovering, knowing, and using mathematical sciences.

Factually, the history of mathematics has been a wild ride of stellar achievement and, now and again, equally dramatic catastrophe. (A gripping example of using math history that will bring students to their feet clamoring for more is Einstein’s Big Idea, an educational film that can viewed on YouTube.)

Let’s ensure our kids see the track of mathematical discovery and development through landmark events in human civilization and (especially) through the minds and lives of the brilliant scientists whose discoveries made these events possible or who applied these discoveries for the benefit of mankind.

The truth is that 100% of primary and secondary school math IS useful. We just have to communicate that truth to our students in such a way that it becomes true for them, too.

Living With Math

∞ PART FOUR ∞

CLARIFY & SIMPLIFY
THE LANGUAGE AND VISUALS

Clarify & Simplify the Language

Especially at lower grades — but whenever necessary for comprehension at any grade level – the language and visuals of Living with Math must be simplified so that examples of use will be quickly grasped by both primary and secondary school students at their grade level. This is a major requirement and one which will challenge the knowledge and ingenuity of authors and illustrators to the max. There is no place in LWM for unusual, exotic, or clever multisyllabic words unless absolutely required by the topic itself. Writers must not be allowed to employ their full vocabularies. The LWM writer’s motto is: “When in doubt, simplify it further.” It does not matter how simplified the examples are or how basic the language and illustrations, so long as the words, pictures, diagrams, and formatting directly communicate the actual use of the math topic in a compelling manner.

Obviously, younger students, whose English is not advanced enough to read even the simplest of examples themselves, will need their applications presented to them via their teachers or tutors, not directly by text. But even here, the words and illustrations should give teachers numerous opportunities for piquing a child’s interest.

Living With Math Glossaries

The written and spoken technical words and symbols of mathematics carry the ideas of the math from teacher and book to the mind of a student. The Living with Math series (both book and video formats) cannot depend upon the glossaries in the back of the student’s math textbook (which are too often woefully incomplete) but must provide its own massive, illustrated glossary of every technical math term used in the book and video series.

Living With Math

∞ PART FIVE ∞

ALGEBRA AND BEYOND

ALGEBRA

AND BEYOND…

Above the concreteness of everyday arithmetic, we find that many of the real-world purposes and uses of algebra and other abstract math subjects require special techniques in order to be successfully communicated to teachers and their students. Make no mistake, there are formidable barriers intrinsic to the process of becoming well-educated in algebra. The simple truth is that the practical knowledge contained in many advanced, abstract math topics can only be attained by undertaking a journey composed of numerous small steps that eventually, at some later date (and sometimes much later), culminate in the ability to do something useful with that knowledge.

For this reason, beyond arithmetic, you frequently cannot provide a student with a complete and detailed example of application for an abstract topic when that specific topic first appears in his curriculum.

Some Algebra 1 topics, like scientific notation, lend themselves to immediately comprehensible real-world applications.

But others do not. The student often does not possess enough knowledge and skill to grasp how a given postulate, property, definition, theorem, rule or algorithm is going to be applied in life. Due to this factor, it can be somewhat tricky to bring to life second-degree polynomial equations (quadratics) when these appear in Algebra 1 courses.

When this limiting factor is the case, however, one does the maximum possible and gives the general area of application, being careful to exclude specifics above the student’s literacy/knowledge level. Instead of specifics that would overwhelm a student, LWM should contain general descriptions of uses with plenty of exciting graphics easily grasped at the student’s current level.

Take quadratic equations:

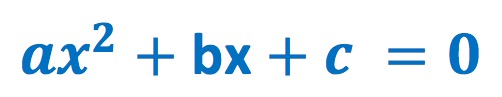
A student who has just learned to recognize and solve a standard-form quadratic equation (ax² + bx + c = 0) and its variations by factoring using the zero-factor theorem, completing the square or using the quadratic formula is not immediately expected to use that math to calculate a planetary orbit or the curvature of a lens. But he still must learn then and there how this data could be applied to the universe of football and heavenly bodies.

One can state and demonstrate in that very first lesson using lively prose, pictures and diagrams, the fact that astronomers do use quadratic equations to determine the orbits of spacecraft and planets.“Aha!” says the student to himself, “now that’s interesting. I think I’ll learn this quadratic stuff because I wouldn’t mind piloting a spaceship when I grow up!” (Jason Thompson, Careers that use Quadratic Equations. eHow. www.ehow.com/info_8711999_careers-use-quadratic-equations.html. Accessed October 29, 2016)

Add another section filled with intriguing words and pictures describing how manufacturers of optical equipment use quadratic equations when designing reflecting telescopes? “Oh, my!” exclaims the student, “I’ve always loved observing the Moon and Mars. Maybe if I learn this quadratic thingy, I can build my own!” (Jason Thompson, Careers that use Quadratic Equations. eHow. www.ehow.com/info_8711999_careers-use-quadratic-equations.html. Accessed October 29, 2016)

And before you exit “Factoring the Quadratic Equation using the Zero-Factor Theorem ” in favor of the next lesson, be sure to let your students know – always and again with plenty of eye-catching, easily-comprehensible images — that auto safety scientists use them to measure stopping distances of automobiles moving at a specific, constant velocity, that the auto safety guys then pass the math results of their tests to the new car designers who use it to develop the right brakes for their new models. “Well”, the student thinks, “being a NASCAR driver is my dream. One day I’ll be rocketing along at 175 mph, and I’m gonna need brakes that work. Hmmm … let me see … now what’s this lesson say about quadratics?” (Jason Thompson, Careers that use Quadratic Equations. eHow. www.ehow.com/info_8711999_careers-use-quadratic-equations.html. Accessed October 29, 2016)

To pique interest further, one can even note that such and certain real-life variable factors fit nicely into the terms of ax² + bx + c = 0, and that, while too advanced for a student’s first lessons on quadratics, particulars on these variables and applications will be taught in ___________ (name and location of source material) when the student reaches that level of math. And you must tell him exactly WHERE the applications can be found, giving the location in specific books and/or videos.

Now that the student knows about real-life applications, knows further the end-products and has been given a bright ray of hope that he himself can attain to that knowledge and skill, you can safely move to the next topic.

There are other techniques for bringing to vibrant life even the driest topic in mathematics, leaving students anticipating their next lesson. To develop additional presentation skills, authors and illustrators of Living with Math need only refer once again to its guiding principles for inspiration:

1) TO MAKE EVERY MATH TOPIC VIVIDLY REAL BY REVEALING ITS USE IN LIFE.

2) TO GIVE TEACHERS AND THEIR STUDENTS SUFFICIENT LEARNING MATERIAL SO THAT THEY CAN CONNECT UP ANY ONE MATH TOPIC TO THE PARTICULAR LIVES OF THEIR INDIVIDUAL STUDENTS.

If the books and videos of Living with Math are executed as described in this paper — with creativity, attention to detail, and love of children — we will send many more young people into worthwhile and exciting careers in such math-intensive fields as accounting, banking, civil engineering, computer design, architecture, biology, astrophysics and aerospace research, students who might otherwise have ended up stocking soup cans in a supermarket when what they really wanted to do with their lives was design skyscrapers or pilot a space craft.

The end

Copyright © 2016, 2017 Bruce Silton

To Be Created

As mentioned earlier in this paper, the comprehensive book and video series described in this paper, Living with Math: Real-World Applications for Primary and Secondary School Mathematics, does not yet exist. This paper, then, is an offer and a call to those individuals and groups who have a strong and continuing interest in creating a future of math literacy for the greatest possible number of individuals.  To be of use to educators and students, the idea must be carried out — actually created, polished, published, and distributed. Individuals and groups who would like to lead or assist with the implementation of LWM are invited to contact the author, Bruce Silton, using the contact page at www.MathCreativity.com.

About the Author

Bruce Silton is a tutor at Clearwater Academy International, a preschool –12^th grede private school in Clearwater, Florida. Since March of 2000, he has delivered approximately 17,000 tutoring sessions. Some 10,000 of those sessions were devoted to helping students overcome difficulties learning math.

The author may be reached through the contact pages of his math educator’s website (MathCreativity.com) or his artist/designer’s website (www.BruceSilton.com).

Editing and proofreading courtesy of Leslie Silton, Book Doctor.

(Note: I added both text and images after Miss Silton’s editing was completed. So I take full responsibility for any errors in this paper.)